统计学：参数估计

浏览量： 886

参数估计是推断统计的重要内容之一。它是在抽样及抽样分布的基础上，根据样本统计量来推断所关心的总体参数。

例如，想知道北京市民的平均收入，最准确的方式就是去询问每个北京市民的收入，然后得到平均值，但实际中往往不可行，因为北京市民的数量太大。所以一般是通过抽样调查以得到样本，统计出样本中的北京市民的平均收入，用这个平均收入去估计整体的平均收入。这就是参数估计。

如果能够获得全部总体的全部数据，那么只需要做一些简单的描述统计，例如，均值、方差、比例等，就可以得到所关心的总体特征，但实际情况往往比较复杂，或者有些总体的个体数很多，不可能对总体中的每个个体都进行测定，这就需要从总体中抽取一部分个体进行调查，进而利用样本提供的信息来推断总体的特征。

参数估计：用样本统计量来估计总体参数，根据对样本指标的计算反应总体指标的情况。

本节课将介绍参数估计的基本方法，主要内容如下。

参数估计的基本原理
一个总体参数的估计
两个总体参数的估计
极大似然估计法

点估计

例如，如果用抽取的部分北京市民的平均收入3000元直接作为全体北京市民的平均收入的估计值，这就是点估计，3000就是点估计值。

点估计是指用样本统计量的某个取值直接作为总体参数的估计值。

弊端：无法给出估计的可靠性的度量。

但实际上，我们一般不会这么做，因为用一个绝对的数值去估计一个东西，很奇怪。一般我们会这样说，大概三四千或者三千左右。

这里的三四千或者三千左右，更多地表示一个范围，其实就是某种区间估计。

在用点估计值代表总体参数值的同时，还必须给出点估计值的可靠性，也就是说，必须能说出点估计值与总体参数的真实值接近的程度。但一个点估计值的可靠性是由它的抽样标准误差来衡量的，这表明一个具体的点估计值无法给出估计的可靠性的度量，因此就不能完全依赖于一个点估计值，而是围绕点估计值构造总体参数的一个区间，这就是区间估计。

区间估计

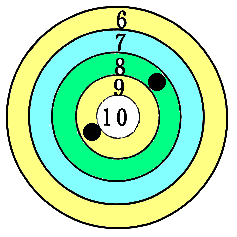
假定参数是靶上10环的位置，作为一次射击，打在靶心10环的位置上的可能性很小，但打在靶子上的可能性就很大，用打在靶上的这个点画出一个区间，这个区间包含靶心的可能性就很大，这就是区间估计的基本思想。

区间估计是在点估计的基础上，给出总体参数估计的一个区间范围，该区间通常由样本统计量加减估计误差得到。

例如，在上方估计北京市民的平均收入的例子中，点估计值是3000，假设估计误差为500，则置信区间为（2500,3500），为了表明估计的可靠性，还需要给出可信度，统计学叫做置信水平。
区间估计示意图如下。

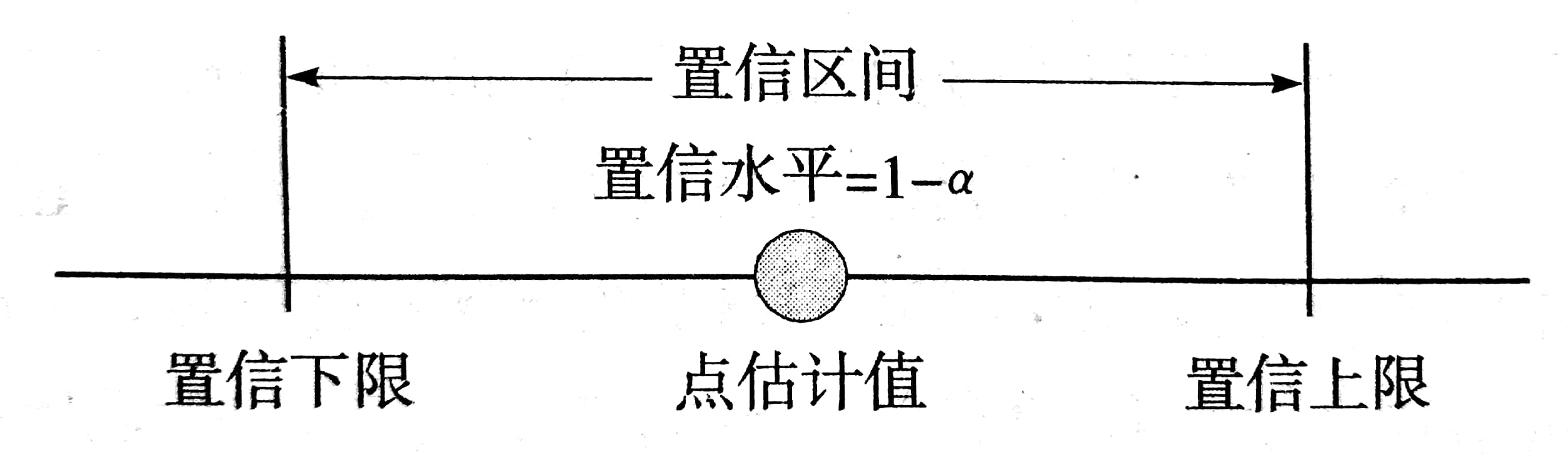
置信区间:由样本统计量所构造的总体参数的估计区间。
置信水平:置信区间中包含总体参数真值的次数所占比例。

一个总体参数的区间估计

研究一个总体时，所关心的参数主要有总体均值、总体比例和总体方差。

正态分布、方差已知，或非正态总体，大样本

当总体服从正态分布且 $\sigma^2$ 已知时，或者总体不是正态分布但为大样本，样本均值 $\overline x$ 的抽样分布均为正态分布，其数学期望为总体均值 $\mu$ ，方差为 $\sigma^2/n$ 。而样本均值经过标准化以后的随机变量则服从标准正态分布，即

$z=\frac{\overline x-\mu}{\sigma/\sqrt n}-N(0,1)$

根据上式和正态分布的性质可以得出总体均值 $\mu$ 在 $1-\alpha$ 置信水平下的置信区间为

$\overline x\pm z_{\alpha/2}\frac{\sigma}{\sqrt n}$

式中， $\overline x-z_{\alpha/2}\frac{\sigma}{\sqrt n}$ 称为置信下限， $\overline x+z_{\alpha/2}\frac{\sigma}{\sqrt n}$ 称为置信上限。
$\alpha$ 是事先所确定的一个概率值，也成为风险值，指总体均值不包括在置信区间的概率， $1-\alpha$ 称为置信水平。
$z_{\alpha/2}$ 是标准正态分布右侧面积为 $\alpha/2$ 时的 $z$ 值；
$z_{\alpha}\frac{\sigma}{\sqrt n}$ 是估计总体均值时的估计误差。

总体均值的置信区间由两部分构成：点估计值和估计误差。

如果总体服从正态分布但 $\sigma^2$ 未知，或总体并不服从正态分布，但是为大样本，可以把式中的总体方差 $\sigma^2$ 用样本方差 $s^2$ 代替，这时

$\overline x\pm z_{\alpha/2}\frac{s}{\sqrt n}$

一个例子：总体均值的区间估计

一家食品生产企业以生产袋装食品为主，每天的产量大约为8000袋。按规定每袋的重量应为100g。为对产品重量进行检测，企业质检部门经常要进行抽样，以分析每袋重量是否符合要求。现从某天生产的一批食品中随机抽取25袋，测得每袋重量如下表所示。

25袋食品的重量单位：g

112.5	101	103	102	100.5
102.6	107.5	95	108.8	115.6
100	123.5	102	101.6	102.2
116.6	95.4	97.8	108.6	105
136.8	102.8	101.5	98.4	93.3

已知产品重量服从正态分布，且总体标准差为10g。试估计该天产品平均重量的置信区间，置信水平为95%。

解答：

已知 $\sigma=10,n=25$ ，置信水平 $1-\alpha=95%$ ,查标准正态分布表，得 $z_{\alpha/2}=1.96$

根据样本数据计算：

$\overline x=\frac{\sum_{i=1}^n x_i}{n}=\frac{2634}{25}=105.36$

根据公式，得

$\overline x\pm z_{\alpha/2}\frac{\sigma}{\sqrt n}=105.36\pm1.96\times\frac{10}{\sqrt 25}$

即

$105.36\pm3.92=(101.44,109.29)$

总体比例

总体方差

这里只讨论正态总体方差的估计问题。

25袋食品的重量单位：g

112.5	101	103	102	100.5
102.6	107.5	95	108.8	115.6
100	123.5	102	101.6	102.2
116.6	95.4	97.8	108.6	105
136.8	102.8	101.5	98.4	93.3

已知产品重量服从正态分布，且总体标准差为10g。试估计该天产品平均重量的置信区间，置信水平为95%。
用之前的数据，以95%的置信水平为建立食品总体重量标准差的置信区间。

两个总体参数的区间估计

两个总体均值之差

两个总体均值之差的估计：独立样本
(1)大样本的估计

如果两个样本是从两个样本中独立抽取的，即一个样本中的元素与另一个样本中的元素相互独立，则成为独立样本。

如果两个总体都为正态分布，或两个总体不服从正态分布但两个样本都为大样本( $n_1\geq30$ 和 $n_2\geq30$ )，根据抽样分布的知识可知，两个总体均值之差 $\overline x_1-\overline x_2$ 的抽样分布服从期望职位( $\mu_1-\mu_2$ )、方差为( $\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}$ )的正态分布，而两个样本均值之差经标准化后则服从标准正态分布，即

$z=\frac{(\overline x_1-\overline x_2)-(\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}服从N(0,1)$

当两个总体的方差 $\sigma_1^2$ 和 $\sigma_2^2$ 都已知时，两个总体均值之差 $\mu_1-\mu_2$ 在 $1-\alpha$ 置信水平下的置信区间为：

$(\overline x_1-\overline x_2)\pm z_{\alpha/2}\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}$

当两个总体的方差 $\sigma_1^2$ 和 $\sigma_2^2$ 未知时，可用两个样本方差 $s_1^2$ 和 $s_2^2$ 来代替，这时，两个总体均值之差 $\mu_1-\mu_2$ 在 $1-\alpha$ 置信水平下的置信区间为：

$(\overline x_1-\overline x_2)\pm z_{\alpha/2}\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}$

某地区教育管理部门想估计两所中学的学生高考时的英语平均分数之差，为此在两所中学独立抽取两个随机样本，有关数据如下表。

中学1	中学2
n1=46	n2=33
$\overline x_1=86$	$\overline x_2=78$
s1=5.8	s2=7.2

根据上面两个样本均值之差的公式，有

$(\overline x_1-\overline x_2)\pm z_{\alpha/2}\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}=(86-78)\pm1.96\times\sqrt{\frac{5.8^2}{46}+\frac{7.2^2}{33}}$

即 $8\pm2.97=(5.03,10.97)$

两个总体比例之差

由样本比例的抽样分布可知，从两个二项总体中抽出两个独立的样本，则两个样本比例之差的抽样分布服从正态分布。
两个样本的比例之差经标准化后则服从标准正态分布。

$Z=\frac{(p_1-p_2)-(\pi_1-\pi_2)}{\sqrt{\frac{\pi_1(1-\pi_1)}{n_1}+\frac{\pi_2(1-\pi_2)}{n_2}}}$

在某个电视节目的收视率调查中，从农村随机调查了400人，有32%的人收看该节目；从城市随机调查了500人，有45%的人收看了该节目。试以95%的置信水平估计城市与农村收视率之差的置信区间。

极大似然估计法

例如，有一个抽奖箱，里面有若干红球和白球，除颜色外，其他一模一样。我们每次从中拿出一个后记录下来再放回去，重复十次操作后发现，有七次抽到了红球，三次是白球，请估计红球所占的比例。

求解：

事件A：重复十次操作后发现，有七次抽到了红球，三次是白球

设红球的比例为 $p$

分布函数： $P(A|M)=P(x_1,x_2,\cdots,x_{10}|M)=P(x_1|M)P(x_2|M)\cdots P(x_{10}|M)=p^7(1-p)^3$

那么 $p$ 在取什么值的时候， $P(A|M)$ 的值最大呢？即求函数的极值。

对 $P(A|M)$ 求导，得

$7p^6(1-p)^3-3p^7(1-p)^2=0$

由以上式子可得

$p=\frac{7}{10}$

也可以取对数

$lnP(A|M)=ln(p^7(1-p)^3)=lnp^7+ln(1-p)^3=7lnp+3ln(1-p)$

$(lnP(A|M))’=\frac{7}{p}-\frac{3}{1-p}=0$

解得