统计学一门关于数据的学科,包括数据收集、处理、分析,从数据中得出结论。数据收集指获得统计数据,数据处理指将数据用图表等形式展示出来,数据分析是指选择适当的统计学方法分析数据,并从数据中得出有用的信息,最后给出结论。
统计学的应用领域非常广泛,例如市场分析、经济预测、财务分析、企业发展战略、产品质量管理等。
##统计数据的类型
统计数据主要三种类型:数值型数据、分类数据和顺序数据。
最常见的数值型数据,用数字来描述事物,现实处理的大多数数据都是数值型数据,例如产品销售额,数值型,而且是连续的数据,例如产品数量,数值型,离散型数据,年龄,数值型,连续型数据。
分类数据主要指类别型数据,例如性别数据,里面都是男或者女,行业数据,里面可能有互联网、汽车、金融、银行、餐饮等。这类数据只是对事物进行分类,并没有顺序。
顺序数据主要是指有顺序的类别变量,例如成绩等级,可以分为及格、良好、优秀等,例如对事物的态度,有不感兴趣、感兴趣、喜欢、非常喜欢等,这类数据除了对事物进行分类之外,还有一个程度的递进。
几个基本概念
统计数据分为数值型、分类型和顺序性,对应的变量也有这三种类型:数值型变量、分类变量和顺序变量,R语言中,分类变量和顺序变量被称为因子。
接着,需要知道总体和样本,参数和统计量(也叫估计量)。
例如,要估计一个班(50人)学生考试的平均分数,从中随机抽取出10人。
这里,全班称为总体,随机抽取的10人就是样本,全班的平均分数称为参数,样本的平均分数是一个统计量。
在数据分析中,需要对数据进行探索性分析,主要有两种形式:一种是通过图表的方式来分析,另一种是通过常用的统计量来分析。
数据探索:图表
数据探索:常用统计量
用于描述数据特征统计量有很多,比如众数、均值、标准差、偏态系数等,这些常用的统计量可以分为三类:集中趋势的度量、离散趋势的度量、偏态和峰态的度量。
第一类:集中趋势的度量
用于集中趋势的度量的统计量有众数、平均数、中位数及四分位数等。下面分别介绍一下。
众数
众数:表示总体中出现次数最多的数值。
例如,在某城市中随机抽取9个家庭,调查得到每个家庭的人均月收入数据如下(单位:元)。
1080 750 1080 1080 850 960 2000 1250 1630
在以上数据中,1080出现的次数最多,出现了3次,所以1080是众数。
当然,可能会有多个众数的情况,例如,有以下数据。
1080 750 1080 850 850 960 2000 1250 1630
1080和850出现的次数相同,都是两次,所以这组数据有两种众数,分别是1080和850。
在Excel中,可以通过函数mode来求众数。
平均数
平均数,其实就是均值,一组数据相加除以数据的个数得到的结果就是均值。
在Excel中,可以通过函数average来求均值。
例如,有数据:
1080 750 1080 1080 850 960 2000 1250 1630
平均数就是所有数字加起来除以数据的个数。
\overline x=\frac{1080+750+1080+1080+850+960+2000+1250+1630}{9}=1186.67
除了均值之外,还有加权平均数、几何平均数。
中位数
将总体中的各个个体数值按照大小顺序排列,居于中间位置的数值,便是中位数。
例如,对于数据:
1080 750 1080 1080 850 960 2000 1250 1630
按照升序排列后,
750 850 960 1080 1080 1080 1250 1630 2000
中间位置上的数据为:1080,所以中位数为1080。
以上数据的个数为9,是一个奇数,所以中位数正好为中间位置上的数字。
如果有偶数个数据,则中位数是中间位置两个数字的平均数。
例如,有以下数据
750 850 960 1080 1080 1080
中间位置上有两个数字,960和1080,中位数为960和1080的平均,即1020。
总结:
- 如果数据为奇数项,中位数是中间位置的数值
- 如果数据为偶数项,中位数是中间位置两个数值的平均数
Excel中,可以通过函数median来求中位数。
四分位数
除了中位数,还有四分位数也表常用。把所有数值由小到大排列并分成四等份,处于三个分割点位置的数值就是四分位数。
例如,有数据:
1080 750 1080 1080 850 960 2000 1250 1630
用Excel公式QUARTILE可以很容易计算四分位数,第一个四分位数:850,第二个四分位数:1080,也就是中位数,第三个四分位数:1500。
Excel中,四分位数位置的确定方法为:
Q_1=\frac{n+3}{4}
Q_3=\frac{3n+1}{4}
按照升序排列后,
750 850 960 1080 1080 1080 1250 1630 2000
根据以上公示,第一个四分位数的位置:(9+3)/4=3,所以第一个四分位数为960,第三个四分位数的位置:(3*9+1)/4=7,所以第三个四分位数为1250。
第二个四分位数就是中位数,前面已经说过。
众数、中位数及平均数的比较
第二类:离散趋势的度量
用于度量离散趋势的统计量有四分位差、极差、方差、标准差等。
四分位差
四分位差也叫四分位距,是第一个四分位数和第三个四分位数之差,用Q_d表示,计算公式为:
Q_d=Q_1-Q_3
四分位差反映了数据中间50%的离散程度,其数值越小,表示数据越集中,数值越大,表示数据越分散。
极差
极差表示一组数据中最大值与最小值之差。
在Excel中,极差没有专门的计算公式,我们可以用max和min分别计算出最大值和最小值,然后作差即可。
方差
方差(variance)反映的数据波动性,用数学语言表示就是,各变量值与其均值离差平方的均值。数学公式为:
var=\frac{\sum_{i=1}^n(x_i-\overline x)^2}{n-1}
标准差
标准差(Standard Deviation)就是方差开方得到。由于方差是在原来数据的基础上进行了平方,所以单位发生了变化,标准差的单位则和原来的数据一致,所以在实际分析时,标准差使用得更多。
偏态与峰态的度量
知道了数据的集中趋势和离散趋势,还想知道数据的分布形状是否对称、偏斜程度,即偏态,分布的偏平程度,也就是峰态,这就需要偏态系数和峰态系数。
偏态系数
偏态(skewness)是对数据分布对称性的测度,如下图所示。
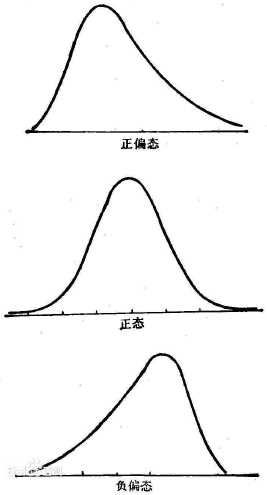
上图中,中间的图为正态,左右对称,最上面的图向右偏,称为正偏态,最下方的图向左偏,称为负偏态。
我们可以通过偏态系数来衡量偏态,计算公式如下。
sk=\frac{n\sum(x_i-\overline x)^2}{(n-1)(n-2)s^3}
其中,s为样本标准差。
在Excel中,通过skew公式可以很容易计算出偏态系数。
当sk>0时,分布是正偏态的。
当sk=0时,分布是对称的。
当sk<0时,分布是负偏态的。
峰态系数
峰态表示数据分布的扁平程度的度量。
例如,不同峰态的分布如下图所示。
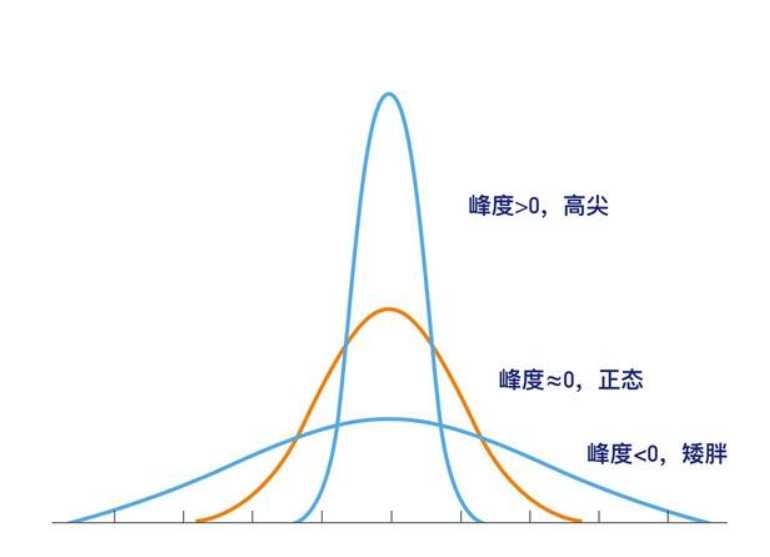
用峰态系数可以衡量峰态。
峰态系数用K来表示,计算公式这里就不给出了,在Excel中,可以通过公式kurt来计算峰态系数。
当K<0时,分布比较高尖,为尖峰分布。
当k>0时,分布比较矮胖,为平峰分布。