线性回归是研究自变量X和因变量y之间的线性关系。
根据自变量X的个数分为一元线性回归(单个自变量)和多元线性回归(多个自变量)。
本节课先学习一元线性回归,在开始学习之前,我们先看一个案例。
一家大型商业银行在多个地区设有分行,其业务主要是进行基础设施建设、国家重点项目建设、固定资产投资等项目的贷款。近年来,该银行的贷款额平稳增长,但不良贷款额也有较大比例的增长,这给银行业务的发展带来较大压力。为弄清楚不良贷款形成的原因,管理者希望利用银行业务的有关数据做些定量分析,以便找出控制不良贷款的办法。
下面是该银行所属的25家分行2002年的有关业务数据。
| 分行编号 | 不良贷款(亿元) | 各项贷款余额 | 本年累计应收贷款(亿元) | 贷款项目个数 | 本年固定资产投资额(亿元) |
|---|---|---|---|---|---|
| 1 | 0.9 | 67.3 | 6.8 | 5 | 51.9 |
| 2 | 1.1 | 111.3 | 19.8 | 16 | 90.9 |
| 3 | 4.8 | 173.0 | 7.7 | 17 | 73.7 |
| 4 | 3.2 | 80.8 | 7.2 | 10 | 14.5 |
| 5 | 7.8 | 199.7 | 16.5 | 19 | 63.2 |
| 6 | 2.7 | 16.2 | 2.2 | 1 | 2.2 |
| 7 | 1.6 | 107.4 | 10.7 | 17 | 20.2 |
| 8 | 12.5 | 185.4 | 27.1 | 18 | 43.8 |
| 9 | 1.0 | 96.1 | 1.7 | 10 | 55.9 |
| 10 | 2.6 | 72.8 | 9.1 | 14 | 64.3 |
| 11 | 0.3 | 64.2 | 2.1 | 11 | 42.7 |
| 12 | 4.0 | 132.2 | 11.2 | 23 | 76.7 |
| 13 | 0.8 | 58.6 | 6.0 | 14 | 22.8 |
| 14 | 3.5 | 174.6 | 12.7 | 26 | 117.1 |
| 15 | 10.2 | 263.5 | 15.6 | 34 | 146.7 |
| 16 | 3.0 | 79.3 | 8.9 | 15 | 29.9 |
| 17 | 0.2 | 14.8 | 0.6 | 2 | 42.1 |
| 18 | 0.4 | 73.5 | 5.9 | 11 | 25.3 |
| 19 | 1.0 | 24.7 | 5.0 | 4 | 13.4 |
| 20 | 6.8 | 139.4 | 7.2 | 28 | 64.3 |
| 21 | 11.6 | 368.2 | 16.8 | 32 | 163.9 |
| 22 | 1.6 | 95.7 | 3.8 | 10 | 44.5 |
| 23 | 1.2 | 109.6 | 10.3 | 14 | 67.9 |
| 24 | 7.2 | 196.2 | 15.8 | 16 | 39.7 |
| 25 | 3.2 | 102.2 | 12.0 | 10 | 97.1 |
这个问题其实是研究各项贷款余额、本年累计应收贷款、贷款项目个数及本年固定资产投资额对不良贷款的影响。
先简化问题,选择各项贷款余额为自变量x,不良贷款为因变量y,绘制x与y的散点图。
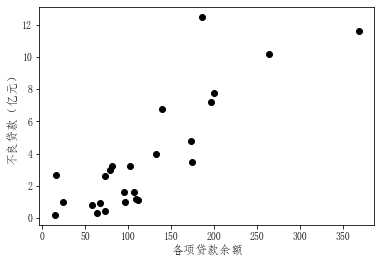
从散点图中可以看到,各项贷款余额与不良贷款之间大体上呈线性关系。
接下来需要找到一条直线(直线方程)来定量地描述这种线性关系。假设拟合直线如下图所示。
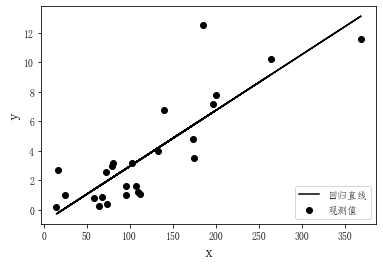
那么,如何确定这条拟合直线呢?
用数学语言表达就是假设回归直线方程为:y=wx+b,如何估计参数w和b?
说明:这里的w是英文单词权重weight的首字母。
一种比较常用的方法就是最小二乘法。
最小二乘法的基本思想是通过最小化这些点到直线的总误差来估计参数w和b。
假定有m个样本,(x_1,y_1),(x_2,y_2),\cdots,(x_m,y_m)。
根据最小二乘法,使
\sum_{i=1}^m(y_i-\hat{y}_i)^2=\sum_{i=1}^m(y_i-wx_i-b)^2
最小。
这个式子采用的是误差的平方和,加上平方是为了避免正负相抵。
在机器学习中,一般将最小化的目标函数成为损失函数(loss function)或者代价函数(cost function)。
现在,损失函数为:
l(w,b)=\sum_{i=1}^m(y_i-wx_i-b)^2
在给定样本数据后,l是w和b的函数,且最小值总是存在。
根据微积分的极值定理,对l求相应于w和b的偏导数,并令其等于0,便可求出w和b,即
\begin{cases}
\frac{\partial{l}}{\partial{w}} =-2\sum_{i=1}^mx_i(y_i-wx_i-b)=0 \\
\frac{\partial{l}}{\partial{b}}=-2\sum_{i=1}^m(y_i-wx_i-b)=0
\end{cases}
解上述方程组得
\begin{cases}
w=\frac{m\sum_{i=1}^mx_iy_i-\sum_{i=1}^mx_i\sum_{i=1}^my_i}{m\sum_{i=1}^mx_i^2-(\sum_{i=1}^mx_i)^2} \\
b=\frac{1}{m}\sum_{i=1}^m(y_i-wx_i)
\end{cases}
在实际问题中,由于计算量较大,一般借助于计算机求解。
接下来的问题是如何评估回归效果?从误差的角度入手。
将由回归方程计算出来的y值记为\hat y,对于每一个实际观测值y_i,其误差的大小用y_i-\hat y_i来表示,所有观测值的总误差可以通过每个观测值的误差的平方和来表示,即
\sum(y_i-\hat y_i)^2
以上式子可以称为误差平方和,或者残差平方和。
我们的目标是找到一个合理的回归方程,使这个误差平方和尽可能小。
如果直接将这个误差平方和作为评估回归模型的指标,不太合适,因为每个回归问题的误差平方和有大有小,没有一个统一的评判标准,所以要接着对误差做一下变形。
y_i-\hat y_i=y_i-\overline y-(\hat y_i-\overline y)
移项得
y_i-\overline y=(y_i-\hat y_i)+(\hat y_i-\overline y)
上式本质上是误差分解,不妨将其称为误差分解式。那么,如何理解这个误差分解式呢?
首先,因变量y的取值是不同的,即在散点图中的表现是波动的,将这种波动称之为变差。对于一个具体的观测值y_i,其变差的大小用y_i-\overline y来表示,也就是误差分解式中左边的部分。
而所有的观测值的总变差可以通过每个观测值的变差的平方和来表示,即
\sum(y_i-\overline y)^2
以上这个式子叫作总变差平方和,简称总平方和。
再看误差分解式的右边,右边第一项前面已经说过,是误差,即我们希望尽可能小的误差。右边第二项,表示回归方程计算出来的y值与y的均值之间的变差,可以理解为回归离差。
所以,我们将总误差分解为了两个方面:一是误差或者残差,我们希望它尽可能小;二是回归离差。
接着,将误差分解式两边平方,并求和,得
\sum(y_i-\overline y)^2=\sum[(y_i-\hat y_i)+(\hat y_i-\overline y)]^2
将右边平方展开,得
\sum(y_i-\overline y)^2=\sum(y_i-\hat y_i)^2+\sum(\hat y_i-\overline y)^2+2\sum(y_i-\hat y_i)(\hat y_i-\overline y)
上式中,可以证明\sum(y_i-\hat y_i)(\hat y_i-\overline y)=0
说明:证明时,需要将\hat y_i=wx+b代入上式中,前面已经求得参数w和b的值。
于是,有
\sum(y_i-\overline y)^2=\sum(y_i-\hat y_i)^2+\sum(\hat y_i-\overline y)^2
在上式中,左边称为总平方和,右边第一项称为误差平方和,右边第二项称为回归平方和,我们的目标是希望误差平方和尽可能小。
在总平方和一定的情况下,回归平方和越大,误差平方和就越小,所以可以借助于回归平方和占总平方和的比例来评估回归方程的好坏,我们将这个比例称之为判定系数,记为R^2,其表达式为:
R^2=\frac{\sum(y_i-\hat y_i)^2}{\sum(y_i-\overline y)^2}=1-\frac{\sum(\hat y_i-\overline y)^2}{\sum(y_i-\overline y)^2}
可以看出,判定系数是一个介于0到1之间的数,判定系数越接近于1,说明回归方程拟合效果越好。
我们已经了解一元线性回归的基本原理,下节课将讲解在Python如何做一元线性回归。