前面我们学习了一元线性回归的原理,本节课用Python实现一元线性回归。
数据读取
首先,读取数据,数据在Excel文件中。
import pandas as pd
bank_data=pd.read_csv("../../data/BankData.csv",index_col="分行编号")
bank_data.head()
运行结果:
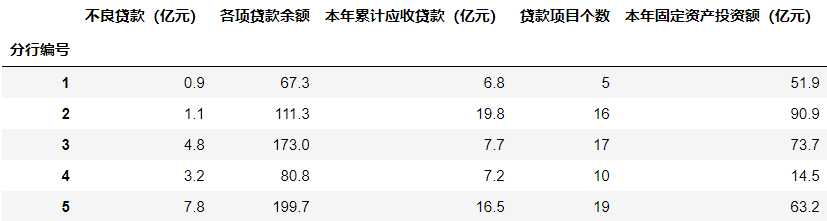
查看数据集的形状。
bank_data.shape
运行结果:
(25, 5)
说明:数据获取方式,关注微信公众号“笨鸟学数据分析”领取!
绘制散点图
前面的理论讲解部分,提到的散点图可以通过Python来绘制,代码如下。
from pylab import mpl
mpl.rcParams['font.sans-serif']=['FangSong'] #指定默认字体
from matplotlib import pyplot as plt
x=bank_data["各项贷款余额"]
y=bank_data["不良贷款(亿元)"]
plt.scatter(x,y,c='black')
plt.xlabel('各项贷款余额',fontsize=12)
plt.ylabel('不良贷款(亿元)',fontsize=12)
plt.show()
运行结果:
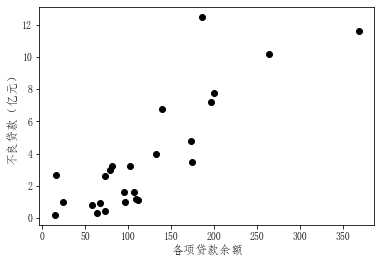
建模
在建模前,需要对数据做一下转换,因为直接通过列名获取到的数据是一维的,不符合sklearn中模型对于数据的要求,转换代码如下。
X=bank_data['各项贷款余额'].values.reshape(-1,1)
y=bank_data['不良贷款(亿元)'].values.reshape(-1,1)
这里.values表示转换为数组,reshape(-1,1)是一种固定写法,1代表列,-1表示不知道几行,这样,就将X和y转换为符合sklearn要求的数组形式。
接着,调用sklearn中的线性回归模型,代码如下。
from sklearn.linear_model import LinearRegression
slModel=LinearRegression()
slModel.fit(X,y)
运行结果:
LinearRegression()
获得判定系数
在线性回归,一般是判定系数来判断模型拟合效果的好坏,判定系数是一个介于0到1之间的数,越接近于1,拟合效果越好。
slModel.score(X,y)
运行结果:
0.7116126467669923
说明模型的拟合效果还算可以。
获得回归方程
接下来,我们获取参数w和b的值,通过coef_属性可以获得w的值,通过intercept_属性可以获得b的值,代码如下。
print(slModel.coef_)
print(slModel.intercept_)
运行结果:
[0.03789471]
-0.8295206165462345
这样,写出回归方程为:
y=-0.83+0.038x
当然,可以调用predict方法给出预测值。
y_pred=slModel.predict(X)
print(y_pred)
运行结果:
[[ 1.72079316]
[ 3.38816027]
[ 5.72626369]
[ 2.23237171]
[ 6.73805236]
[-0.21562636]
[ 3.24037091]
[ 6.19615805]
[ 2.81216072]
[ 1.92921405]
[ 1.60331957]
[ 4.18015964]
[ 1.39110921]
[ 5.78689522]
[ 9.15573467]
[ 2.17552965]
[-0.26867895]
[ 1.95574034]
[ 0.10647865]
[ 4.45300153]
[13.12331049]
[ 2.79700284]
[ 3.32373927]
[ 6.60542089]
[ 3.04331843]]
这个预测值实际上是根据回归方程计算得到的,有了这个预测值,就可以在散点图中加上拟合直线了,代码如下。
fig,ax=plt.subplots()
ax.scatter(x,y,c='black',label="观测值")
ax.plot(x,y_pred,'black',label="回归直线")
plt.legend(loc="lower right")
plt.xlabel('x',fontsize=16)
plt.ylabel('y',fontsize=16)
plt.show()
运行结果:
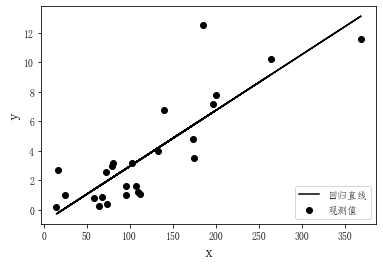
以上就是用Python做一元线性回归。