前面学习了一元线性回归,本节课我们来学习多元线性回归,多元线性回归的基本原理和一元线性回归类似,只是涉及到多个自变量。
一元线性回归是要找一条直线去拟合样本点,而多元线性回归要找到一个超平面去拟合样本点。
我们可以想像如果是在三维空间中,需要找到一个平面去拟合样本点,如下图所示。
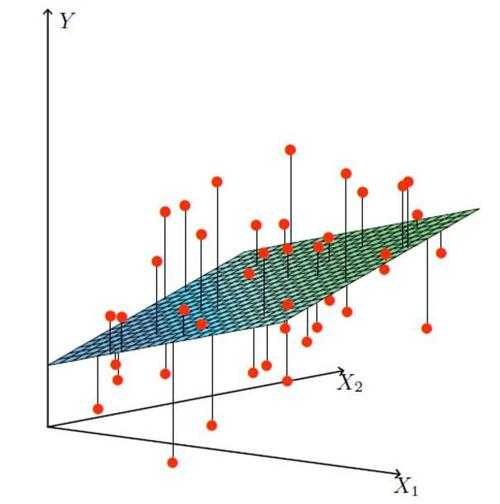
在上图中可以看到,每个样本点和拟合平面之间都存在一个误差,我们要找的平面就是总误差最小的那个平面,这正是最小二乘法的思想。
在更高维的空间中,这个平面被称之为超平面。
设多元线性回归方程为:
y=w_1x_1+w_2x_2+…+w_nx_n+b
如何估计参数?还是用最小二乘法。
假定有m个样本,(x_1,y_1),(x_2,y_2),\cdots,(x_m,y_m)。
注意:n个参数,m个样本。
损失函数:
l(w_0,w_1)=\sum_{i=1}^m(y_i-w_1x_i-w_2x_i-…-w_nx_i-b)^2
根据微积分的极值定理,对l求相应于w_1,w_2,…,w_n和b的偏导数,并令其等于0,即
\begin{cases}
\frac{\partial{l}}{\partial{w_i}} =-2\sum_{i=1}^mx_i(y_i-w_1x_i-w_2x_i-…-w_nx_n-b)=0,i=1,2,…,n\\
\frac{\partial{l}}{\partial{b}}=-2\sum_{i=1}^m(y_i-w_1x_i-w_2x_i-…-w_nx_n-b)=0
\end{cases}
解上述方程组可以得到各参数的值。
对于多元线性回归,还可以将其方程写成矩阵的形式。
跟一元线性回归一样,由于计算量较大,一般借助于计算机求解。