决策树初步

决策树，顾名思义，是用树状图来模拟人的决策行为的一种算法，本质上是一系列if/else问题。
例如，金融机构判断是否考虑给一个人放贷，可能考虑的因素有：房子、工作、信贷情况及年龄等。其决策流程大致为：

1. 房子：是否有房？如果有房，则考虑放贷。如果没房，则继续考虑工作情况。
2. 工作：在没有房子的情况下，如果有工作，则考虑放贷，否则继续考虑信贷情况。
3. 信贷情况：在没有工作的情况下，如果信贷情况非常好，考虑放贷，否则不考虑放贷。

当然，这只是一个简单的模拟决策，实际问题要复杂很多。我们可以将以上决策流程用以下树状图来描述。

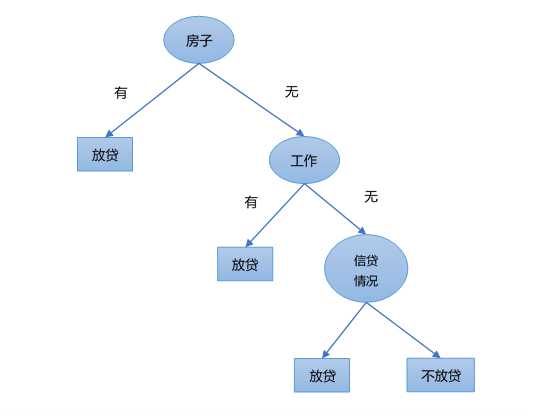
上图中，用来描述决策过程的树状图称为决策树，决策树的第一个节点称为根节点，用于描述中间过程的节点称为内部节点，代表最终决策结果的节点称为叶子节点。

那么，凭什么选择房子作为根节点？
假设有一份金融机构借贷数据集，样本是需要借贷的人，有没有房子、有没有工作、信贷情况怎么样等则是样本的特征，是/否放贷是样本的类别标签。
选择某个特征作为根节点，其实就是用这个特征将样本数据集划分成了两部分，即有房子的样本数据集和没有房子的样本数据集。
所以接下来的问题是，如何划分一个数据集？
先别着急，我们需要先了解一些基础概念。

熵

例如，有两个数据集D1和D2。
D1={男，男，女，男，女，女}
D2={男，男，女，男，男，男}
数据集D1对我们说来是混乱的，因为不同性别标签的样本都混在一起，数据集D2相对不那么混乱的，因为其中的大部分样本都是一种性别，男，尽管有一个性别标签为女的样本。
那么，如何衡量一个数据集的混乱程度呢？
答案是熵，熵在信息论中很常见，可以用来衡量数据的混乱程度，表示信息的期望值。
对于数据集D1来说，包含两个类别，男和女。对于男这个类别来说，其出现的概率记为p_1=\frac{3}{6}，接着，取一个底为2对数并加一个负号，表示该类别的信息值，即l(男)=-\log_2p_1=1
按照同样的方式，可以计算出女这个类别的信息值，即l(女)=-\log_2p_2=1
接着，计算整个数据集的所有类别的信息期望值，就是数据集D1的熵，记为
H(D_1)=-p_1\times\log_2p_1-p_2\times\log_2p_2=1
对于数据集D2来说，也可以按照类似的方式计算出它的熵，即
H(D_2)=-p_1\times\log_2p_1-p_2\times\log_2p_2=-\frac{5}{6}\times\log_2\frac{5}{6}-\frac{1}{6}\times\log_2\frac{1}{6}=0.65
从上面可以看到，数据集D1的熵明显大于数据集D2的熵，即数据集D1的混乱程度大于数据集D2。

以上计算过程涉及两个概念：某个分类的信息和熵。

1. 某个类别的信息，定义为：l(x_i)=-\log_2p(x_i)，其中，p(x_i)表示选择该类别的概率。
2. 熵，数据集中所有类别的信息期望值，用公式表示为：H(X)=-\sum_{i=1}^n{p(x_i)\log_{2}p(x_i)}，其中，n是类别数目。对于常见的二分类问题，n=2。

对于一个二分类问题来说，只有两个类别，整个数据集的熵的计算公式为：

H(X)=-p\log_2(p)-(1-p)\log_2(1-p)

将H(X)看成是一个关于p的函数，画出它的函数图像如下。

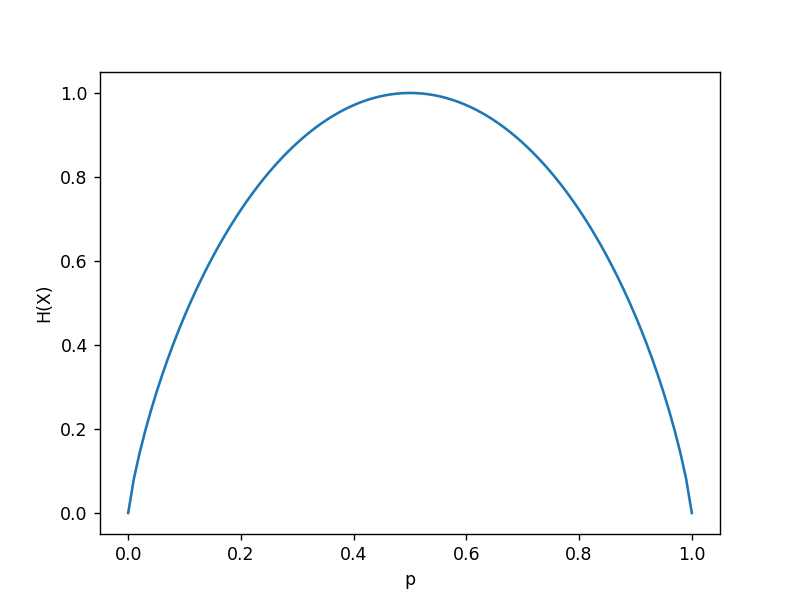
上图中，当p=0.5时，H(X)达到最大值1，当p=0或者p=1时，H(X)达到最小值0。
也就是说，假设一个数据集中有两个类别（二分类问题），当这两个类别各占一半时，熵是最大的，等于1，当只有一个类别时，它的熵最小，为零。
了解了熵之后，接着来说说划分数据集。划分数据集的基本原则是：将无序的数据变得有序。说白了就是将混在一起的数据尽可能按照类别分开。

在划分数据集前后信息发生的变化称为信息增益，为了说明信息增益，我们给数据集D加上一个特征头发。
例如，有以下数据集D，共有6个样本，每个样本有一个特征：头发，有一个类别标签，即性别，取值为男或者女。

编号	头发	性别
1	短发	男
2	长发	男
3	长发	女
4	短发	男
5	长发	女
6	短发	女

首先，计算出数据集D的总体熵经验条件熵，记为H(D|A)

H(D|A)=\frac{3}{6}\times H(D_1)+\frac{3}{6}\times H(D_2)=0.92

可以看到，数据集划分前后，信息发生了变化，我们将其称为信息增益，记为g(D,A)。

g(D,A)=H(D)-H(D|A)=1-0.92=0.08

好，相信大家已经理解了经验条件熵和信息增益，概括一下。
经验条件熵表示按照某特征划分数据集后，各子数据集的熵按照其占总体的比例之和，简称为条件熵。
信息增益表示划分数据集前后，信息发生的变化，即总体熵-条件熵。

决策树构造基本步骤

了解了这些基本概念后，可以尝试构造一个决策树，决策树构造的基本步骤分为以下4步。

1. 计算整个数据集的总体熵
2. 计算各个特征的条件熵、信息增益（总体熵-条件熵）
3. 选择信息增益最大的特征为分类节点
4. 以此类推，构造出整个决策树

决策树构造实例

有以下金融机构借贷数据，共有15个样本，每个样本有4个特征：年龄、是否有工作、是否有房子和信贷情况，有1个类别标签：是/否放贷。

ID	年龄	有工作	有自己的房子	信贷情况	类别
1	青年	否	否	一般	否
2	青年	否	否	好	否
3	青年	是	否	好	是
4	青年	是	是	一般	是
5	青年	否	否	一般	否
6	中年	否	否	一般	否
7	中年	否	否	好	否
8	中年	是	是	好	是
9	中年	否	是	非常好	是
10	中年	否	是	非常好	是
11	老年	否	是	非常好	是
12	老年	否	是	好	是
13	老年	是	否	好	是
14	老年	是	否	非常好	是
15	老年	否	否	一般	否

现在我们需要根据以上样本数据构造一个决策树。

第1步：计算整个数据集的总体熵。

H(D)=-\frac{9}{15}\times\log_2\frac{9}{15}-\frac{6}{15}\times\log_2\frac{6}{15}=0.971

第2步：计算各个特征的条件熵、信息增益（总体熵-条件熵）

考虑特征年龄，根据特征年龄A_1，将数据集D划分为三部分D1,D2,D3，如下图所示。

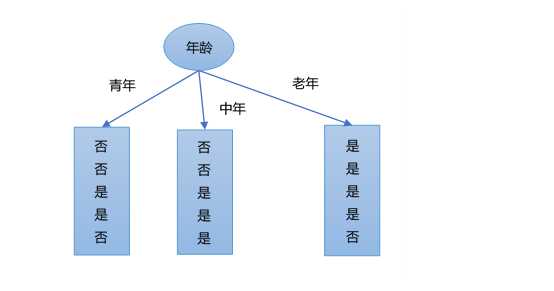
接着，计算这三部分的熵，分别为：

H(D_1)=-\frac{3}{5}\log_2(\frac{3}{5})-\frac{2}{5}\log_2(\frac{2}{5})=0.971

H(D_2)=-\frac{2}{5}\log_2(\frac{2}{5})-\frac{3}{5}\log_2(\frac{3}{5})=0.971

H(D_3)=-\frac{1}{5}\log_2(\frac{1}{5})-\frac{4}{5}\log_2(\frac{4}{5})=0.723

根据数据集D，年龄分别取青年、中年、老年的概率为：\frac{5}{15},\frac{5}{15},\frac{5}{15}

经验条件熵：H(D|A_1)=\frac{5}{15}H(D_1)+\frac{5}{15}H(D_2)+\frac{5}{15}H(D_3)=0.888

信息增益：g(D,A_1)=H(D)-H(D|A_1)=0.971-0.888=0.083

考虑特征是否有工作，根据特征工作A_2，将数据集D划分为两部分D1,D2，如下图所示。

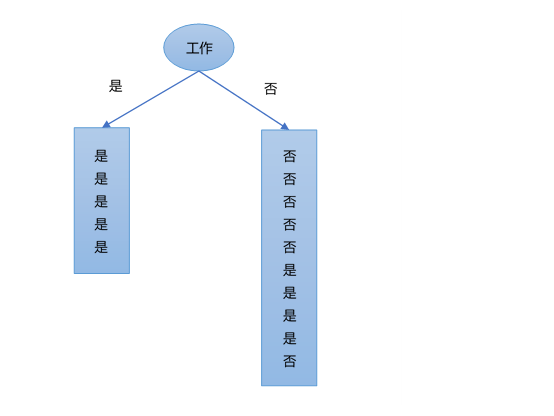
接着，计算这两部分的熵，分别为：

H(D_1)=-\frac{5}{5}\log_2(\frac{5}{5})=0

H(D_2)=-\frac{4}{10}\log_2(\frac{4}{10})-\frac{6}{10}\log_2(\frac{6}{10})=0.971

根据数据集D，工作分别取是、否的概率为：\frac{5}{15},\frac{10}{15}

经验条件熵：H(D|A_2)=\frac{5}{15}H(D_1)+\frac{10}{15}H(D_2)=0.647

信息增益：g(D,A_2)=H(D)-H(D|A_2)=0.971-0.647=0.324

考虑特征是否有房，根据特征是否有房A_3，将数据集划分为两部分，如下图所示。

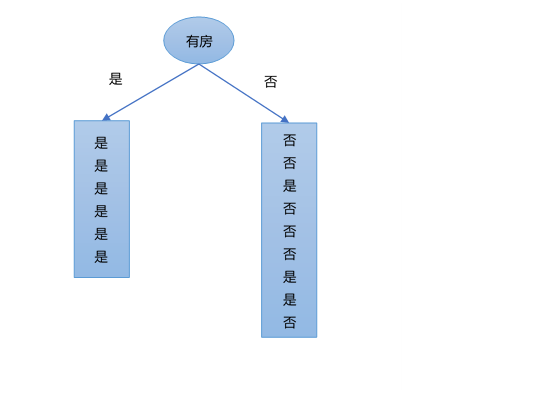
接着，计算其信息增益为：

g(D,A_3)=H(D)-H(D|A_3)=0.971-[\frac{6}{15}(-\frac{6}{6}\log_2\frac{6}{6})+\frac{9}{15}(-\frac{3}{9}\log_2\frac{3}{9}-\frac{6}{9}\log_2\frac{6}{9})]=0.971-0.551=0.420

考虑特征信贷情况A_4，根据这个特征将数据集划分为三部分，如下图所示。

接着，计算其信息增益为：

g(D,A_4)=H(D)-H(D|A_4)=0.971-0.608=0.363

最后，比较各特征的信息增益值，特征A_3(有房)的信息增益值最大，所以选择特征A_3作为最优特征，即根节点。这就回答了本文开始的问题，“凭什么选择房子作为根节点？”。

对于根据特征”有房”得到的数据集D_2继续使用如上方法，可以构造出如下决策树。

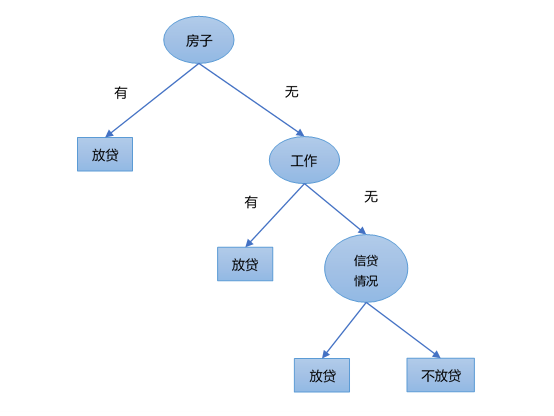
以上构造决策树的方法被称为ID3算法，即在决策树各节点上应用信息增益准则选择特征，递归构建决策树。

常用的决策树算法

除了ID3算法，还有C4.5算法、CART算法等。
总结一下，常用的决策树算法有：

• ID3：在决策树各节点上应用信息增益准则选择特征，递归构建决策树。问题：存在偏向于选择取值较多的特征的问题。
• C4.5：对ID3算法进行了改进，用信息增益比来选择特征。
• CART：分类与回归树，有特征选择、树的生成及剪枝组成，既可以用于分类也可以用于回归。

当然，如果只是为了使用决策树去解决数据分析问题，可以先不用关心这些算法的细节，因为sklearn中有现成的实现，我们需要根据不同的参数去调用不同的决策树算法即可。

树的剪枝

通常来说，一个完整的决策树会遍历所有特征，这样会导致模型过于复杂，对于训练集的分类很准确，但是对于未知数据集的分类却没那么准确，即存在过拟合的现象。所以，需要控制决策树的复杂度，即决策树的剪枝，防止过拟合风险。

将已生成的树进行简化的过程称为剪枝（pruning），剪枝通常有两种策略：

• 预剪枝：提前控制树的生长，当熵减少的数量达到某一个阈值时，就停止树的分支的生成。
• 后剪枝：先构造一棵树，然后删除信息较少的分支。

对于只关注应用的同学来说，只需要关注sklearn中的决策树工具中的相关参数即可。
这里列出几个。

• max_depth 数据少或者特征少的时候可以不管这个值，如果模型样本量多，特征也多的情况下，可以尝试限制下。
• max_leaf_nodes 通过限制最大叶子节点数，可以防止过拟合，默认是”None”，即不限制最大的叶子节点数。如果加了限制，算法会建立在最大叶子节点数内最优的决策树。如果特征不多，可以不考虑这个值，但是如果特征分成多的话，可以加以限制具体的值可以通过交叉验证得到。

决策树的可视化

现在假设我们得到了一个决策树，可以通过工具graphviz将决策树可视化。可视化效果如下图所示。

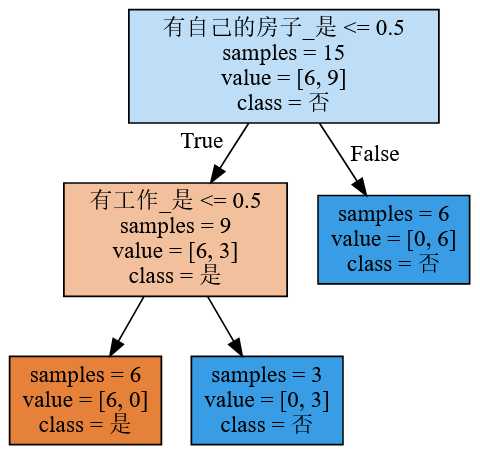
为了实现决策树可视化，需要安装两个东西：Graphviz软件和graphviz库。

安装Graphviz软件

首先下载Graphviz软件，下载地址：http://www.graphviz.org/
下载之后，双击安装包，不断“下一步”即可。

安装graphviz库

使用pip命令安装graphviz库即可。

安装好之后，即可通过Python代码实现决策树的可视化。
以上就是决策树的基本原理及可视化。