逻辑回归

之前说的线性回归是预测一个连续的数值，比如金融机构根据工资、住房、年龄等预测一个放贷量。
线性回归： y=w_1x_1+w_2x_2+ \cdots + 𝑤_nx_n+b

而还有一类问题是预测类别，比如，根据工资、住房、年龄等预测是否给一个人放贷。
这种预测类别的问题就要用到逻辑回归。

逻辑回归主要步骤

1. 连续转为离散：sigmoid函数
2. 写出损失函数
3. 应用梯度下降求解损失函数

连续转为离散

h_w(x_1,x_2,…,x_n)=w_1x_1+w_2x_2+…+w_nx_n+b

写成向量的形式

\vec x=\begin{bmatrix} x_1&x_2&\cdots&x_n&1 \end{bmatrix} ~~~~~~~~~~ \vec w=\begin{bmatrix} w_1 \\ w_2 \\ \vdots \\ w_n \\ b \end{bmatrix}

说明：

• 为了表示的方便，这里将\vec x扩充了一个特征1。
• 为了表示的方便，将w也进行乐扩充，增加一个b。

从数学的角度来看，h_w(x_1,x_2,…,x_n)是两个向量的内积。

数学中，两个向量的内积直接乘起来就好了，但是，在Python中，向量也是作为矩阵来处理，以矩阵的形式来运算，所将其写为矩阵的乘法。

\begin{bmatrix}w_1,w_2,\cdots,w_n,b\end{bmatrix} \times\begin{bmatrix}x_1\\x_2\\ \vdots\\x_n\\1\end{bmatrix}

h_w(x)=w^T x=w_1x_1+w_2x_2+…+w_nx_n+b

由于线性回归输出的是一个数值，无法直接解决二分类问题，那么如何改进线性回归模型来预测类别呢？

我们可以采用概率的方法去预测类别为A的概率，设置阈值为0.5，如果得到类别为A的概率大于0.5，则属于类别A，反之属于类别B。

由于概率是一个[0,1]之间的连续数值，所以要找到一个函数，将线性回归的连续值映射到[0,1]上的连续值。

一个最直接的办法就是设定一个阈值，比如0，如果预测的y>0，那么属于类别A，否则属于类别B，这种模型也被称为感知机（Perception）。

sigmoid函数

由于概率是一个[0,1]之间的连续数值，所以要找到一个函数，将线性回归的连续值映射到[0,1]上的连续值。

这个函数就是sigmoid函数：

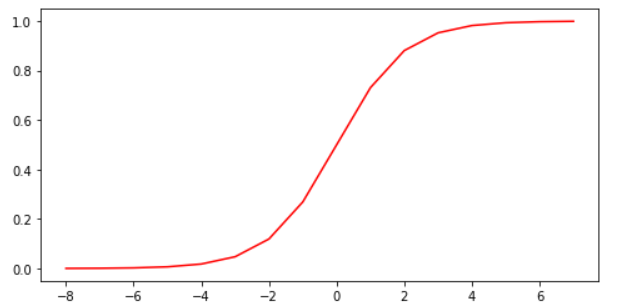
f(x)=\frac{1}{1+e^{-x}}

sigmoid函数的图像如下所示。

将线性回归函数h_w(x)=w^T x代入sigmoid函数，得

f(h_w(x))=\frac{1}{1+e^{-w^Tx}}

损失函数

接下来写出这个函数的损失函数。

假设预测结果只有两个类别（标签），1和0，y=1的概率为p，y=0的概率为1-p，则

\begin{cases}
P(y=1|x;w)=f(h_w(x))=\frac{1}{1+e^{-w^Tx}}=p\\
P(y=0|x;w)=1-p
\end{cases}

为了方便计算，将这个函数统一为以下形式：

P(y|x;w)=p^y(1-p)^{1-y}

在上式中，当y=1时，结果是p，当y=0时，结果是1-p。

假设现在采集到了m个样本，其似然函数为：

L(w)=P=P(y_1|x_1;w)P(y_2|x_2;w)\cdots P(y_m|x_m;w)=\Pi_{i=1}^mp^{y_i}(1-p)^{1-y_i}

说明：对于独立事件来说，概率乘积表示这些事件同时发生的概率，所以似然函数可以理解为一个总的概率。

但是，由于相乘的式子不好计算，所以通过取对数，将乘法变成加法，得到对数似然函数

lnL(w)=ln(\Pi_{i=1}^mp^{y_i}(1-p)^{1-y_i})=\sum_{i=1}^m{lnp^{y_i}(1-p)^{1-y_i}} \\
=\sum_{i=1}^m({y_ilnp+(1-y_i)ln(1-p))}

其中，p=\frac{1}{1+e^{-w^Tx}}

接着要求这个似然函数（损失函数）的最大值，此时如果直接用梯度来求解最大值，就叫作梯度上升了。

为了跟其他机器学习问题统一，即最小化损失函数，引入函数l(w)=-\frac{1}{m}lnL(w)作为损失函数，此时将求解最大值问题转化为了求解最小值问题，故应用梯度来求解这个最小值的过程就叫作梯度下降法。

除以m表示平均损失。

接下来，计算损失函数l(w)的梯度。

\frac{\partial l(w)}{\partial w_j}=\frac{\partial}{\partial w_j}(-\frac{1}{m}lnL(w))=-\frac{1}{m}\frac{\partial lnL(w)}{\partial w_j} \\
=-\frac{1}{m}\sum_{i=1}^m({y_i\frac{1}{p}\frac{\partial p}{\partial w_j}+(-1)(1-y_i)\frac{1}{1-p}\frac{\partial p}{\partial w_j})}

上式中提到了p关于参数w_j的导数，由于p也是一个复合函数，所以下面先求\frac{\partial p}{\partial w_j}

\begin{aligned}
\frac{\partial p}{\partial w_j}&=\frac{\partial}{\partial w_j}(\frac{1}{1+e^{-w^Tx}}) \\
&=\frac{1}{(1+e^{-w^Tx})^2}*(-1)*e^{-w^Tx}*(-x_{ij}) \\
&=\frac{1}{(1+e^{-w^Tx})^2}*e^{-w^Tx}*x_{ij} \\
&=\frac{1}{1+e^{-w^Tx}}*\frac{e^{-w^Tx}}{1+e^{-w^Tx}}*x_{ij} \\
&=p(1-p)x_{ij}
\end{aligned}

总之，得到一个结论：\frac{\partial p}{\partial w_j}=p(1-p)x_{ij}

于是，接着之前的计算：

\begin{aligned}
\frac{\partial l(w)}{\partial w_j}
&= -\frac{1}{m}\sum_{i=1}^m({y_i\frac{1}{p}\frac{\partial p}{\partial w_j}+(-1)(1-y_i)\frac{1}{1-p}\frac{\partial p}{\partial w_j})}\\
&=-\frac{1}{m}\sum_{i=1}^m{{y_i\frac{1}{p}p(1-p)x+(-1)(1-y_i)\frac{1}{1-p}p(1-p)x}}\\
&=-\frac{1}{m}\sum_{i=1}^m{{y_i\frac{1}{p}p(1-p)x+(-1)(1-y_i)\frac{1}{1-p}p(1-p)x}}\\
&=-\frac{1}{m}\sum_{i=1}^m(y_i-p)x
\end{aligned}

将p=\frac{1}{1+e^{-w^Tx}}代回，得

\frac{\partial l(w)}{\partial w_j}=-\frac{1}{m}\sum_{i=1}^m(y_i-\frac{1}{1+e^{-w^Tx}})x

接下来，迭代求解参数的值，给参数设置一个初始值，然后通过不断更新参数使损失函数（梯度加了负号）减小。

参数更新的表达式为：

w_i=w_i-\alpha\frac{\partial}{\partial w_i}l(w_0,w_1,…,w_n)=w_i+\alpha\frac{1}{m}\sum_{i=1}^m(y_i-\frac{1}{1+e^{-w^Tx}})x

说明：这里的减号表示梯度下降。

接下来通过计算工具例如Python进行多次迭代。