ARIMA预测模型原理篇

时间序列是日常生活中非常常见的数据，例如餐馆每天的销售数据、股票行情数据、中国近10年的GDP数据等，这些数据都有一个共同点，都是随时间的变化而变化。

时间序列基本概念

时间序列，英文名叫time series，时间序列数据有两个要素：时间和数值型指标。
说明：这里的时间是一个统称，包含年份、季度、月份、天、时、分、秒等。
例如，餐馆每天的销售额数据如下表所示。

日期	销量
2015-01-01	3023.01
2015-01-02	3039.01
2015-01-03	3056.01
2015-01-04	3138.01
2015-01-05	3188.01

餐馆每天的销售数据就是一个时间序列，销量按照日期排列而成。
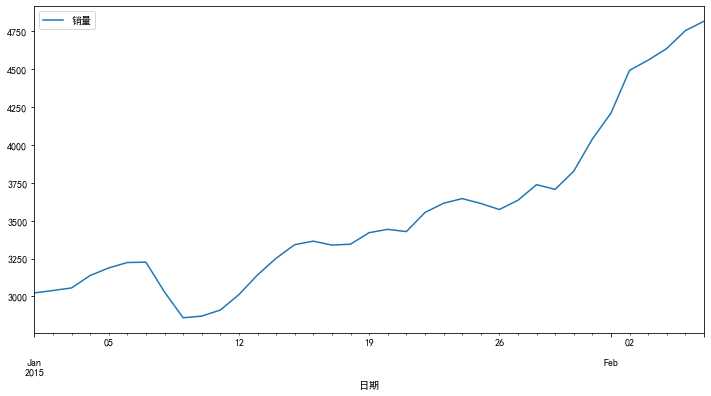
对于时间序列数据来说，一般通过折线图来反映数据随时间变化的趋势，如下图所示。

平稳序列和非平稳序列

时间序列按照是否存在趋势分为平稳序列和非平稳序列。
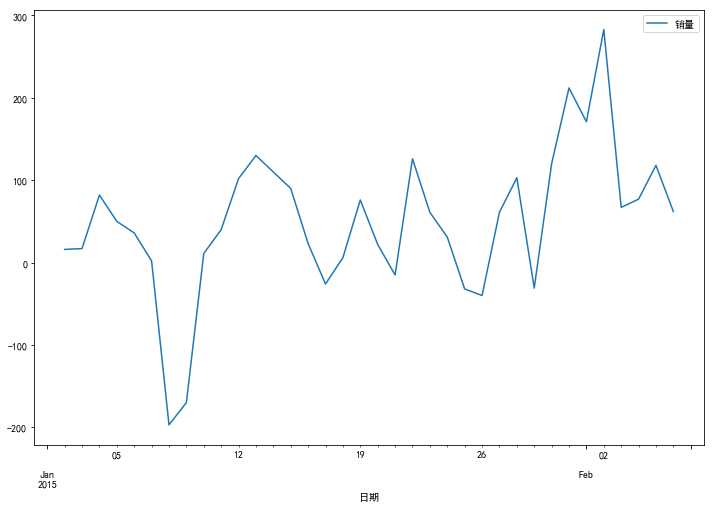
平稳序列指基本不存在趋势的序列，如下图所示，虽然不断波动，但总体没有上升或者下降的趋势。

非平稳序列指包含趋势的序列，如下图所示，虽然波动，但总体呈上升趋势。

说明：严格地说，非平稳序列是指包含趋势、季节性或周期性的序列。

说了这么多，ARIMA到底是神马？ARIMA是Autoregressive Integrated Moving Average Model的缩写，中文翻译：自回归移动平均模型。
ARIMA可以拆分为AR+I+MA三部分，其中AR代表一个模型，MA代表一个模型，I代表差分。
下面分别介绍这三部分：差分，MA模型和AR模型。

差分

对于非平稳序列，可以通过差分转化为平稳序列。
差分简单来说，就是将时间序列中连续的两项做差（后一项减去前一项），得到的差值构成一个新的序列。
用数学语言表达为：

c_t=y_t-y_{t-1}

做一次差分就叫一阶差分，记差分阶数d为1。
做两次差分也叫二阶差分，记差分阶数d为2。
三次、四次等同理。
通常，对于一个非平稳序列来说，做一次差分就能够去除其中的线性趋势，从而变成一个平稳序列。
由于大多数时间序列预测模型基本都是基于平稳序列的，所以以下讨论的时间序列模型都有一个前提条件，那就是基于平稳序列，对于非平稳序列，通过差分将其转化为平稳序列。

MA模型

MA是英文moving average的缩写，即移动平均，所以MA模型叫作移动平均模型。
移动平均是指将时间序列表示为一系列不相关的随机变量的线性组合，这一系列不相关的随机变量我们称之为白噪声。
用数学语言表达，就是：

y_t=\theta_1e_{t-1}+\theta_2e_{t-2}+\cdots+\theta_qe_{t-q}+e_t

其中，y_t表示第t期的观测值，\theta_i表示加权系数，\{e_{t-q}\}表示白噪声序列。
用通俗的话来说，现在的你是由过去不断地犯错所造成的。
当q取1时，则为一阶移动平均，用数学语言表达为：

y_t=\theta_1e_1+e_t

当q取2时，则为二阶移动平均，用数学语言表达为：

y_t=\theta_1e_{t-1}+\theta_2e_{t-2}+e_t

一般情况下，三阶移动平均即可搞定问题。
那么问题来了，阶数q值如何确定？
为了回答这个问题，这里不得不提到自相关这个概念。
自相关就是自己和自己的相关性，说白了就是时间序列中各个观测值之间的相关性。
将这些自相关系数构成的图叫作自相关函数图，英文名称叫作AutoCorrelation Function Plot，简称ACF图。
ACF图长啥样呢？就是下面这个图。

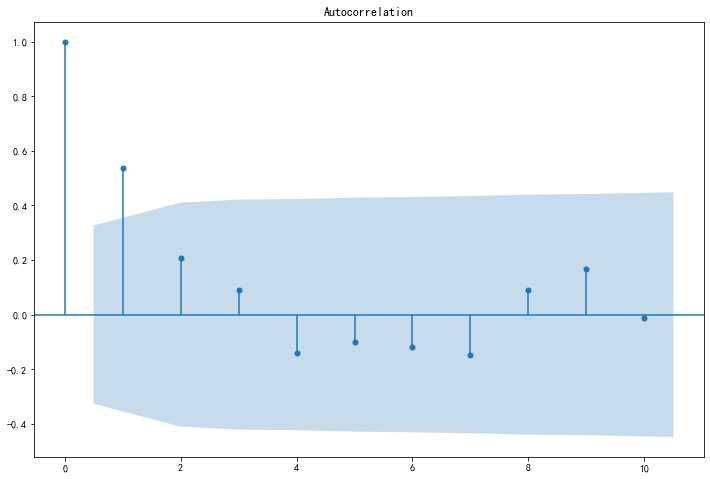
上图中，横坐标表示阶数，纵坐标表示相关系数的大小。随着阶数的增加，自相关系数会不断变化，时而为正，时而为负，总体趋势是不断变小。
从上图中可以看出，在阶数q=2之后，自相关系数会落在一个带状区域中。

AR模型

AR是英文autoregressive的缩写，即自回归，所以AR模型叫作自回归模型。
自回归，顾名思义，就是用自身的历史数据去预测自身。用数学语言表达，就是：

y_t=\phi_1y_{t-1}+\phi_2y_{t-2}+\cdots+\phi_py_{t-p}+e_t

其中，y_i表示第i期的观测值，\phi_i表示回归系数，或加权系数，e_t表示误差项,p表示阶数，AR(p)表示p阶自回归。
用通俗的话来说，就是现在的你，是由过去的你不断创造的。
当p取1时，则为一阶自回归，用数学语言表达为：

y_t=\phi_1y_{t-1}+e_t

当p取2时，则为二阶自回归，用数学语言表达为：

y_t=\phi_1y_{t-1}+\phi_2y_{t-2}+e_t

一般情况下，三阶自回归即可搞定问题。
那么问题来了，p值如何确定？
为了回答这个问题，这里要提到偏自相关的概念。
偏自相关是指剔除了中间k-1个随机变量（y_{t-1},y_{t-2},\cdots,y_{t-k-1}）的干扰后，y_t和y_{t-k}之间的相关性。
偏自相关图，英文名称为artial AutoCorrelation Function Plot，简称PACF图。
PACF图如下所示。

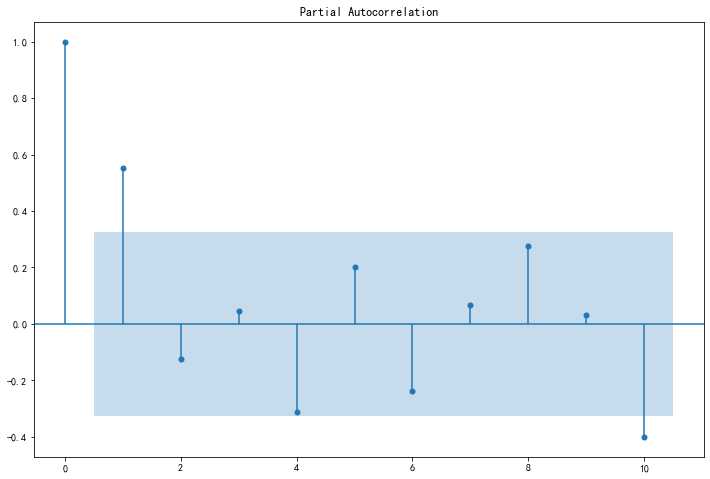
上图中，横坐标表示阶数k，纵坐标表示偏自相关系数的大小。随着阶数的增加，偏自相关系数会不断变化，时而为正，时而为负，总体趋势是不断变小，在阶数p=2之后，偏自相关系数会落在一个带状区域中。
总结一下，确定参数q和p的方法如下表所示。

模型	ACF	PACF
ARIMA(p,d,0)	逐渐减小到零	在p阶后减小到零
ARIMA(0,d,q)	q阶后减小到零	逐渐减小到零
ARIMA(p,d,q)	逐渐减小到零	逐渐减小到零

ARIMA模型

ARIMA模型就是将以上所讲的工具综合在一起，形成了一个强大的预测工具。
假定现在有一个非平稳序列需要预测，我们将它交给ARIMA模型。
ARIMA模型拿到后，会这样处理：
首先，进行差分，将其转化为一个平稳序列，确定参数d。
接着，绘制ACF图和PACF图，确定参数q和p的值。
最后，根据残差、AIC/BIC等评估模型。

这就是ARIMA模型的基本原理，下节课我们将会用Python演示一个ARIMA模型案例。