支持向量机这个名称来自于英文翻译,support vector machine,简称SVM。
SVM基本原理
支持向量机主要用于解决分类问题。
假设有m个样本点(\vec x_1,y_1),(\vec x_2,y_2),\cdots,(\vec x_m,y_m),y_i\in\begin{Bmatrix}-1,+1\end{Bmatrix},作出散点图,如下图所示,我们希望找到一条最优直线将两组数据分开。
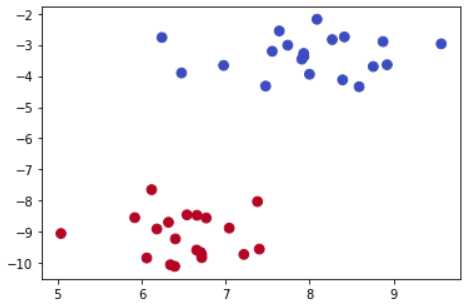
用于分隔的直线可以有很多条,这里作出两条分隔直线,如下图所示。
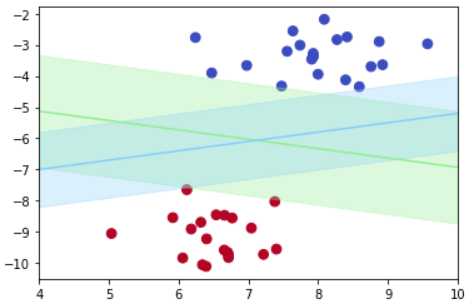
从图中可以看到,分隔直线到样本点边界有一定的距离,这个距离越大,说明分隔直线分类出错的可能性就越小,所以我们的目标是寻找这个距离最大的分隔直线。
接着,我们需要了解SVM中的几个关键概念。这里给出一个SVM的示意图。
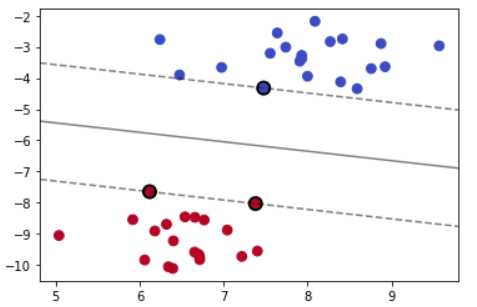
上图中,中间的黑色分隔直线叫作分隔直线,在三维空间中叫作分隔平面,在高维空间中就叫作分隔超平面(hyperplane);分隔之间两侧有两条虚线,这两条虚线之间的距离叫作间隔(margin);两条虚线上的样本点叫作支持向量(support vector)。
SVM模型
现在,我们的目标是寻找最大间隔。
任意分隔超平面可以用以下这个线性方程来描述:
w^Tx+b=0
从几何角度看SVM
根据几何知识,任意样本点x=(x_1,x_2,…,x_n)到直线w^Tx+b=0的距离公式为:
\frac{|w^Tx+b|}{||w||}
其中,||w||=\sqrt{w_1^2+w_2^2…+w_n^2}
假设间隔为d,我们的目标是最大化这个距离d,这相当于目标函数,用数学式子表达为:
\max\limits_{w,b}~d
而对于其他点到平面的距离则要求大于等于\frac{d}{2},样本边界的点(支持向量)使等号成立,这相当于约束条件。
对于类别+1,即y_i=+1,要求\frac{w^Tx_i+b}{||w||}\geq \frac{d}{2};
对于类别-1,即y_i=-1,要求\frac{w^Tx_i+b}{||w||}\leq -\frac{d}{2}
即
\begin{cases}
\frac{w^Tx_i+b}{||w||}\geq+\frac{d}{2} \quad y_i=+1 \\
\frac{w^Tx_i+b}{||w||}\leq-\frac{d}{2} \quad y_i=-1
\end{cases}
说明:样本边界的点(支持向量)使等号成立。
接下来,将这两个类别的约束条件合起来,写成一个式子,即
y_i\times\frac{w^Tx_i+b}{||w||}\geq \frac{d}{2}
仔细看上面这个式子,无论y_i=+1还是y_i=-1,都满足上面给出的约束条件。
对于样本边界的点(支持向量),有以下式子成立。
y_i\times\frac{w^Tx_i+b}{||w||}=\frac{d}{2}
由于上式是从几何角度得出的,不放将其称为几何支持向量等式。
从函数角度看SVM
以上是从几何的角度来考虑SVM问题,接下来从函数的角度来考虑SVM问题。
已知分隔超平面的方程为:
w^Tx+b=0
考虑函数f(x)=w^Tx+b
若是超平面能够正确地分类样本,则对于类别1,即当y_i=1时,w^Tx_i+b>0,对于类别-1,即当y_i=-1时,w^Tx_i+b<0。
为了方便接下来的讨论,在保持分隔超平面方程w^Tx+b=0不变的情况下,可以对函数w^Tx+b进行缩放,使其满足当y_i=1时,w^Tx_i+b\geq1,当y_i=-1时,w^Tx_i+b\leq-1,样本边界的点(支持向量)使等号成立。
所以,对于样本边界的点(支持向量),有以下式子成立。
y_i\times(w^Tx_i+b)=1
结合之前得出的“几何支持向量等式”,有
d=\frac{2}{||w||}
这样做对于接下来目标函数的优化没有影响,则约束条件变成:
所以,目标函数变为:
\max\frac{2}{||w||}
约束条件变为:
y_i\times(w^Tx_i+b)\geq1 \ ,i=1,2,\cdots,m.
但是,对于机器学习问题来说,一般都是求损失函数(目标函数)的最小值,又因为最大化\frac{2}{||w||}和最小化\frac{||w||}{2}等价,为了方便计算,加上一个平方去除根号,即得\frac{1}{2}||w||^2。
所以将以上目标函数变为\min\frac{1}{2}||w||^2,于是,得到下面这个优化问题:
\begin{aligned}
& \min\frac{1}{2}||w||^2 \\
& s.t. \quad y_i(w^Tx_i+b)\geq1 \ ,i=1,2,\cdots,m.
\end{aligned}
其中,||w||=\sqrt{w_1^2+w_2^2…+w_n^2}
说明:s.t.是subject to (such that)的缩写,受约束的意思。
SVM优化问题求解
接下来,求解这个SVM优化问题,本质上是一个不等式约束优化问题。
已知SVM优化问题为:
\begin{aligned}
& \min\frac{1}{2}||w||^2 \\
& s.t. \quad y_i(w^Tx_i+b)\geq1 \ ,i=1,2,\cdots,m.
\end{aligned}
接下来开始求解,大致步骤为:
- 第1步:构造拉格朗日函数
- 第2步:利用强对偶性转换
- 第3步:利用SMO算法求解二次规划问题
- 第4步:求解参数w和b,得到超平面方程,即最大分隔超平面。
第一步:构造拉格朗日函数
L(w,b,\lambda)=\frac{1}{2}||w||^2+\sum_{i=1}^m\lambda_i[1-y_i(w^Tx_i+b)] \quad s.t. \ \lambda_i\geq0
假设找到了目标函数的最小值p,即\frac{1}{2}||w||^2。
在上面的式子中,右边第二项\sum_{i=1}^n\lambda_i[1-y_i(w^Tx_i+b)]\leq0,因为\lambda\geq0。
所以有L(w,b,\lambda)\leq p,为了找到最优的参数\lambda,使得L(w,b,\lambda)接近p,所以问题转换为\max\limits_{\lambda}L(w,b,\lambda)。
于是,之前的优化问题可以转换为:
\min\limits_{w,b}~\max\limits_{\lambda}L(w,b,\lambda) \quad s.t. \ \lambda_i\geq0
第二步:利用强对偶性转换
利用强对偶性,将以下目标函数转化为:
\max\limits_\lambda\min\limits_{w,b}L(w,b,\lambda)
求解参数w和b,对参数求偏导,得
\begin{aligned}
&\frac{\partial L}{\partial w}=w-\sum_{i=1}^n\lambda_ix_iy_i=0\\
&\frac{\partial L}{\partial b}=\sum_{i=1}^n\lambda_iy_i=0
\end{aligned}
由以上方程可得
w=\sum_{i=1}^n\lambda_ix_iy_i, \quad \sum_{i=1}^n\lambda_iy_i=0
将以上结果代入第一步构造的拉格朗日函数,可得:
\begin{aligned}
L(w,b,\lambda)&=\frac{1}{2}||w||^2+\sum_{i=1}^n\lambda_i[1-y_i(w^Tx_i+b)]\\
&=\frac{1}{2}||\sum_{i=1}^n\lambda_ix_iy_i||^2+\sum_{i=1}^n\lambda_i-\sum_{i=1}^n\lambda_iy_i(w^Tx_i+b)\\
&=\frac{1}{2}||\sum_{i=1}^n\lambda_ix_iy_i||^2+\sum_{i=1}^n\lambda_i-\sum_{i=1}^n\lambda_iy_iw^Tx_i+\sum_{i=1}^n\lambda_iy_ib\\
&=\frac{1}{2}||\sum_{i=1}^n\lambda_ix_iy_i||^2+\sum_{i=1}^n\lambda_i-\sum_{i=1}^n\lambda_iy_i(\lambda_ix_iy_i)x_i+\sum_{i=1}^n\lambda_iy_ib\\
\end{aligned}
好了,观察一下上面的式子,第一项和第四项都为零,于是得到一个仅含参数\lambda的式子
L(\lambda)=\sum_{i=1}^n\lambda_i-\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\lambda_i\lambda_jy_iy_j(x_ix_j)
第三步:利用SMO算法求解二次规划问题,求解参数
于是,得到这样二次规划问题:
\max L(\lambda)=\max[\sum_{i=1}^n\lambda_i-\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\lambda_i\lambda_jy_iy_j(x_ix_j)] \quad s.t. \quad \sum_{i=1}^n\lambda_iy_i=0,\lambda_i\geq0
这种二次规划问题一般采用SMO(Sequential Minimal Optimization)算法求解。
SMO算法,中文名称为序列最小优化算法,核心思想:每次优化一个参数,其他参数固定。
对于以上这个优化问题,无法每次只优化一个参数,因为有一个约束条件\sum_{i=1}^n\lambda_iy_i=0,如果每次优化一个\lambda,其他\lambda固定,则这个待优化的\lambda将不再是变量,因为它可以有其他固定的\lambda推出,所以对于这个问题,每次选取两个\lambda优化。
优化的具体步骤为:
1、选择两个需要优化的参数\lambda_i和\lambda_j,其他参数固定。
此时,约束条件变成:\lambda_iy_i+\lambda_jy_j=c,\lambda_i\geq0,\lambda_j\geq0,其中,c=-\sum_{k\neq i,j}\lambda_ky_k,由此可以得出\lambda_j=\frac{c-\lambda_iy_i}{y_i},也就是说,其实我们可以用\lambda_i表达\lambda_j,这样就把这个优化问题变成了仅有一个约束条件的优化问题,这个唯一的约束条件是\lambda_i\geq0。
2、对这个优化问题,对参数\lambda_i求导,可以得到\lambda_i的一个值,进而还可以得到\lambda_j的一个值。
3、重复步骤1,2,即多次迭代,直至函数收敛。
第四步:求解参数w和b,得到超平面方程,即最大分隔超平面
在利用强对偶性转换中,通过求偏导,得到w=\sum_{i=1}^n\lambda_ix_iy_i,通过这个式子可以得到w。
接着,求参数b。随便找一个支持向量(边界点)(x_0,y_0)代入方程y_0(w^Tx_0+b)=1,解出b即可。
b=y_0-w^Tx_0
为了使模型更加具有鲁棒性,可以求得支持向量的均值。
b=\frac{1}{n}\sum_{i=1}^n(y_i-w^Tx_i)
至此,参数w和b都求出来了,于是得到分割超平面的方程。
软间隔(soft margin)
前面我们的推导都基于线性可分的情况,但是在实际应用中,完全线性可分的样本是很少的,总有一些异常点,如下图所示。
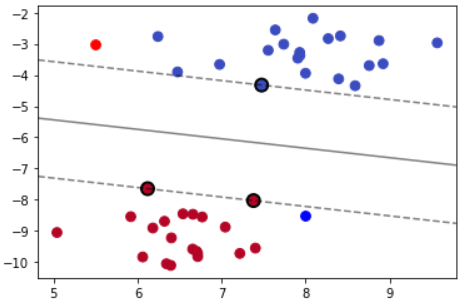
为了解决这个问题,我们为每个样本引入一个松弛变量\xi_i ,令\xi_i\geq0 ,且 1-y_i(w^Tx_i+b)-\xi_i\leq0。
这里需要说明两点:
- 异常点里间隔边界越远,其松弛变量\xi_i 的值就越大。
- 对于正常点来说,其松弛变量\xi_i 的值等于0,即满足y(w^Tx+b)\geq1
为了跟之前的间隔平面区分,将之前比较严格的间隔称为硬间隔,此时的间隔平面称为软间隔。
增加软间隔后,优化目标变成了:
\begin{aligned}
\min \frac{1}{2}||w||^2+C\sum_{i=1}^m\xi_i \quad s.t.\ g_i(w)=1-y_i(w^Tx_i+b)-\xi_i\leq0,\xi_i\geq0,i=1,2,\dots,n
\end{aligned}
其中 C 是一个大于 0 的常数,可以理解为对错误样本的惩罚程度.
- C 越大, \xi_i就越小,说明有较少的异常点跨过间隔边界,此时模型也就越复杂。
- C越小,\xi_i就越大,说明有较多的异常点跨过间隔边界,此时模型也就越简单。
接下来求解这个新的优化问题。
第一步:构造拉格朗日函数
\begin{aligned}
& \min\limits_{w,b,\xi}\max\limits_{\lambda,\mu}L(w,b,\lambda,\xi,\mu)=\frac{1}{2}||w||^2+C\sum_{i=1}^m\xi_i+\sum_{i=1}^n\lambda_i[1-\xi_i-y_i(w^Tx_i+b)]- \sum_{i=1}^n\mu_i\xi_i \\
& s.t.\ \lambda_i\geq0,\mu_i\geq0
\end{aligned}
其中,\lambda_i和\mu_i是拉格朗日乘子,w,b和\xi_i是目标函数的参数。
第二步:利用强对偶性,得到对偶问题
根据强对偶性,得到原始问题的对偶问题:
\max\limits_{\lambda,\mu}\min\limits_{w,b,\xi}L(w,b,\lambda,\xi,\mu)
接下来,对于这个对偶问题,求解参数。
第三步:利用SMO算法求解参数\lambda
分别对参数w,b和\xi_i求偏导数,并令偏导数等于0,得
w-\sum_{i=1}^m\lambda_iy_ix_i=0 \\
\sum_{i=1}^m\lambda_iy_i=0 \\
C-\lambda_i-\mu_i=0
将这些关系式代入拉格朗日函数中,得
\max\limits_{\lambda,\mu}\min\limits_{w,b,\xi}L(w,b,\lambda,\xi,\mu)=\sum_{i=1}^n\lambda_i-\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\lambda_i\lambda_jy_iy_j(x_ix_j)
由于这个式子中,只剩下\lambda了,所以优化问题变为:
\max\limits_{\lambda}[\sum_{i=1}^n\lambda_i-\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\lambda_i\lambda_jy_iy_j(x_ix_j)]\\
s.t. \sum_{i=1}^n\lambda_iy_i=0,\lambda_i\geq0,C-\lambda_i-\mu_i=0
接着,利用SMO算法求解参数\lambda。
第四步:求解参数w和b,得到超平面,即最大分割超平面
在利用强对偶性转换中,通过求偏导,得到w=\sum_{i=1}^n\lambda_ix_iy_i,通过这个式子可以得到w。
接着,求参数b。随便找一个支持向量(边界点)(x_0,y_0)代入方程y_0(w^Tx_0+b)=1,解出b即可。
b=y_0-w^Tx_0
为了使模型更加具有鲁棒性,可以求得支持向量的均值。
b=\frac{1}{n}\sum_{i=1}^n(y_i-w^Tx_i)
至此,参数w和b都求出来了,于是得到分割超平面的方程。
说明:间隔内的噪声点也属于支持向量。
从线性可分到线性不可分
前面,我们讨论的都是线性可分,或者大部分线性可分(软间隔)。
实际问题中,有些样本是无法线性可分的,如下图示。
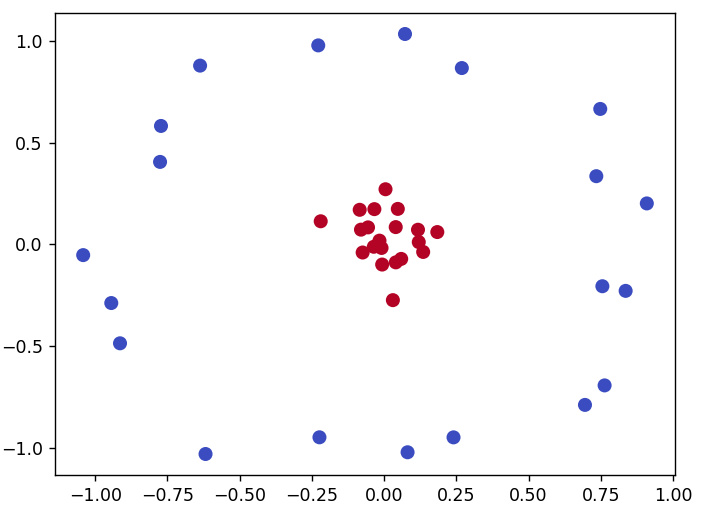
这种在二维空间中无法线性可分的问题,增加一个特征,可以将其映射到三维空间(高维空间),在高维空间中,可以找到一个平面分隔这些样本,于是,样本点便线性可分。

用一个平面将这些样本分隔开
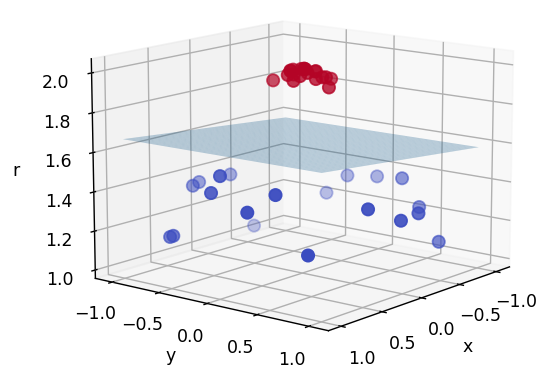
那么,接下来的问题便是找到一个新的函数,将原来的样本点映射到高维空间。
假设找到一个新的函数\phi(x),它能够将原来的样本点x映射到新的高维空间,那么超平面的方程为:f(x)=w\phi(x)+b
此时,非线性SVM的对偶问题为:
\max\limits_\lambda[\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\lambda_i\lambda_j(\phi(x_i)\cdot\phi(x_j))-\sum_{j=1}^n\lambda_i]\\
s.t. \quad \sum_{i=1}^n\lambda_iy_i=0,\lambda_i\geqq0,C-\lambda_i-\mu_i=0
可以看到,这个对偶问题的公式跟之前的唯一不同在于:(x_i\cdot x_j)变成了(\phi(x_i)\cdot\phi(x_j))
说明:对偶问题公式参考前面的对偶推导。
虽然看起来这只是一点点的不同,但是当将样本点映射到高维空间后,计算量会变得很大。
核函数
为了解决计算量的问题,引入核函数。
设想有一个函数k(x_i,x_j)=\phi(x_i)\cdot\phi(x_j),这样就将计算\phi(x_i)\cdot\phi(x_j)转化为计算函数k(x_i,x_j)的值,而不必计算高维空间中\phi(x_i)的内积。
这个函数称之为核函数。当然,可以通过数学证明核函数一定存在。
于是,非线性SVM的对偶问题就转化为:
\max\limits_\lambda[\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\lambda_i\lambda_jk(x_i,x_j)-\sum_{j=1}^n\lambda_i]\\
s.t. \quad \sum_{i=1}^n\lambda_iy_i=0,\lambda_i\geqq0,C-\lambda_i-\mu_i=0
这样,就能够以较小的计算量求解这个非线性SVM优化问题。
常见的核函数有高斯核函数、线性核函数及多项式核函数等。
高斯核函数
高斯核函数也叫rbf核,其全称为径向基函数(Radius Basic Function),表达式如下。
k(x_i,x_j)=\exp(-\frac{||x_i-x_j||^2}{2\sigma^2})=\exp(-\gamma||x_i-x_j||^2)
rbf核表达式中涉及两个样本点的距离计算,距离可以理解为两个样本点的相似程度。
\gamma是sklearn中的svm库中的另外一个参数,对于参数\gamma可以这样理解。
- $\gamma$越大,意味着两个样本点比较接近时才会被判定为相似,这样决策边界会变得较为扭曲,容易发生过拟合。
- $\gamma$越小,意味着两个样本点容易被判定为相似,此时模型较为简单,容易发生欠拟合。
总结:SVM中的两个重要参数
•参数C:与软间隔相关
•参数\gamma:与核函数相关