在之前的机器学习模型中,我们都是用精度来评估模型。除了进度之外,还有一些其他的评估指标。
之前已经说过,一个二分类问题包含两个类别,正类和负类(或者叫反类)。
例如,在乳腺癌肿瘤预测这个二分类问题中,如果我们感兴趣的是类别为恶性的样本,则把恶性称为正类,良性称为负类。
两类错误
对于一个模型来说,总会有预测错误的时候。预测出错有两种可能性。
第一种:将一个类别为良性(正类)的样本预测为恶性(反类),这就叫作假正类,也叫第一类错误。
第二种:将一个类别为恶性(反类)的样本预测为良性(正类),就叫作假反例,也叫第二类错误。
混淆矩阵
对于一个二分类问题来说,类别标签有两个类别,预测结果有两个类别,
样本的类别标签中,正类记为positive class,负类记为negative class。
预测结果中,预测正类记为predicted positive,预测负类记为predicted negative。
样本的实际类别和预测类别组合一下,共有四种情况。
负类样本被预测为负类,称为真负类(true negative,TN)
负类样本被预测为正类,称为假负类(flase negative,FN)
正类样本被预测为负类,称为假正类(false positive,FP)
正类样本被预测为正类,称为真正类(true positive,TP)
将这四种情况用一个矩阵来表示,如下图所示。
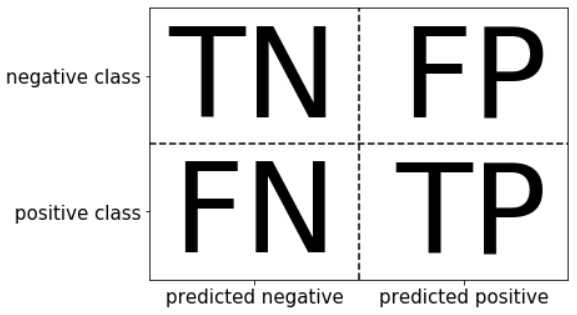
上面这个矩阵被称为混淆矩阵(confusion matrix)。
对于二分类问题来说,混淆矩阵是一个2\times2的矩阵(或者数组)。
在这个矩阵中,四个方块中的数字加起来等于样本总数。正对角线上的TN+TP是预测正确的样本个数,反对角线上的FP+FN是预测错误的样本数。
回想一下精度,精度(Accuracy)表示预测正确的样本个数除以样本总数,所以有以下公式:
Accuracy=\frac{TN+TP}{TN+TP+FP+FN}
从上面可以看到,精度只是混淆矩阵中反映出来的一个信息,除了精度之外,还有另外两个指标,准确率和召回率。
准确率(Precision)表示被预测为正类的样本中有多少是真正类,计算公式如下。
Precision=\frac{TP}{TP+FP}
例如,在乳腺癌肿瘤这个案例中,我们希望对恶性样本用药物进行临床试验,也就是对被预测为正类的样本进行药物治疗,众所周知,这类药物一般非常昂贵,所以为了减少试验成本,被预测为正类的样本中有多少是真正的正类是非常重要,也就是准确率要非常高才可以。
召回率(Recall)表示正类样本中有多少被预测为正类,计算公式如下。
Recall=\frac{TP}{TP+FN}
召回率也叫作灵敏度(sensitivity)。
例如,在乳腺癌肿瘤这个案例中,我们希望找到尽可能多的恶性样本,从而避免错过治疗,哪怕找出的样本中含有部分良性样本,此时,正类样本中有多少被预测为正类就很重要,也就是召回率要非常高才好。
绘制混淆矩阵
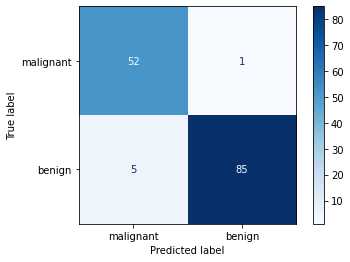
我们可以通过sklearn中的plot_confusion_matrix方法来绘制混淆矩阵。
from sklearn.metrics import plot_confusion_matrix
disp = plot_confusion_matrix(lg_model, X_test, y_test,
cmap='Blues', values_format='d',
display_labels=cancer.target_names)
绘制出来的混淆矩阵效果如下图所示。
再次回顾准确率和召回率。
Precision=\frac{TP}{TP+FP}
Recall=\frac{TP}{TP+FN}
观察准确率的式子,分析:
如果预测少量确定的样本点为正类,其他均预测为负类,此时,假正类为零,即FP=0,可以得到100%的准确率。但是假负类会很多,即FN会很大,此时,召回率就会很低。
反过来,如果预测所有的样本均为正类,则没有假负类,即FN=0,可以得到100%的召回率,但是假正类会很多,即FP会很大,此时,准确率会很低。
所以,准确率和召回率不能只考虑其中一个指标,我们需要将两个指标结合起来考虑。
准确率-召回率曲线
为了同时考虑准确率和召回率,一种方式就是绘制准确率-召回率曲线。
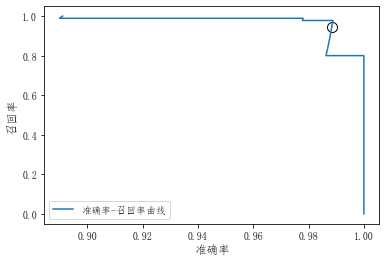
上图中,黑色的圆圈表示阈值为0的点,这个点是调用predict方法时所选择的折中点。
要想准确率和召回率都很高,则曲线应该靠近右上角的位置。
这条曲线下的面积,叫作平均准确率,这个值越大,表示预测效果越好。
ROC曲线
在机器学习中,还有一个常用工具用于评估模型的预测效果,ROC曲线。
ROC是receiver operating characteristics curve的简称,中文名称是受试者工作特性,ROC曲线,即ROC curve,就是受试者工作特性曲线。
ROC曲线考虑的是假正例率(false positive rate,FPR)和真正例率(true positive rate,TPR),真正例率其实就是之前说过的召回率,假正例率表示假正类占所有负类样本的比例,公式为:
FPR=\frac{FP}{FP+TN}
ROC曲线如下图所示。
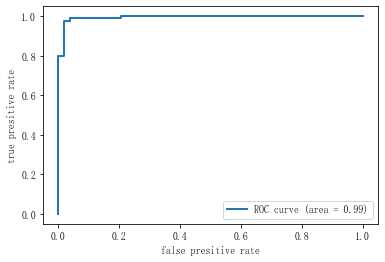
对于ROC曲线来说,越靠近左上角,表示模型的预测效果越好。
ROC曲线下的面积,即area under the curve,简称AUC,我们可以用AUC值来衡量模型的预测效果,AUC值越大,则模型的预测效果越好。