什么是函数?
函数,英文名是function,所以取首字母f表示函数,一般表示为f(x),这里的x表示自变量。
考虑生活中的现象,路程等于速度乘以时间,假设速度恒定,对于不同的时间,就会对应不同的路程,这是一个最简单的数学问题,用s表示路程,v表示速度,t表示时间,则有关系式:s=vt。
在这个关系式中,t叫作自变量(自己变化),s叫作因变量(因自变量而变化),这两个变量形成的关系称为函数,记为f(t)=vt。
将时间t的取值看成是一个集合,路程s的取值看成是一个集合,按照法则f将时间t映射到路程s上,所以,函数可以看成是一种映射,本质是变量之间的关系。
又比如,圆的面积公式:S=\pi r^2,半径r是自变量,面积S是因变量,给定一个半径r,就有一个唯一的面积S与之对应,这也是一个函数关系式。
上面说的两个函数,自变量的取值都必须大于等于零,例如时间t只能取大于等于零的数,半径r也是如此,必须大于等于零,自变量的取值范围叫作函数的定义域,对应的因变量的取值范围叫作值域,显然,上面这两个函数的值域也是大于等于零。
函数中的自变量通常用x来表示,因变量用y来表示,函数关系式用y=f(x)表示,不同的函数,函数关系式也不同。
总结一下,函数的定义:
设x和y是两个变量,D是一个给定的非空实数集合,如果对于任意x属于D,按照一定的法则,变量y总有唯一确定的值与之对应,则称变量y是变量x的函数,记作y=f(x),其中x称作自变量,y称作因变量。
举个例如,y=1也是一个函数,只是这个函数比较特殊,无论自变量x取什么值,因变量的值都是1,这种函数也称为常数函数。
这里要注意的是对于每一个自变量x,都有一个唯一确定的y与之对应,尽管它们都相等。
分段函数
函数家族中有很多成员,其中一种叫分段函数。
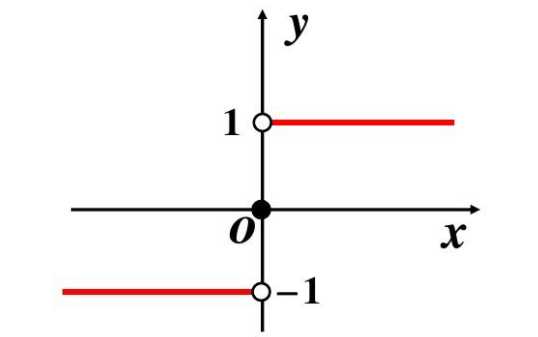
例如,函数:
H(x)=\begin{cases}
-1,x<0, \\
0,x=0, \\
1,x>0
\end{cases}
这个函数,不用的x取值将函数值分成了三段,我们称之为分段函数。图像如下。
反函数
反函数,就是函数的逆过程,例如根据时间求路程是一个函数,反过来,根据路程求时间就是反函数。
t=\frac{s}{v}
一般地,y=f(x),x\in D的反函数记为:f^{-1}(y)=x,x\in f(D).
复合函数
复合函数就是两个函数复合构成一个新的函数.
例如,函数u(x)=(x+1)^2,其中y=x+1本身就是一个函数,记为g(x)=x+1,而平方可以看作是函数f=x^2,函数u(x)可以看作是函数g(x)和函数f(x)的复合函数。
复合函数的概念为:
设函数y=f(u)的定义域为D_f,函数u=g(x)的定义域为D_g,且其值域R_g\subset D_f,则由下式确定的函数
y=f[g(x)],x\in D_g
称为由函数u=g(x)与函数y=f(u)构成的复合函数,它的定义域为D_g,变量u称为中间变量。
常见的初等函数
在初高中数学中,即所谓的初等数学,学习了很多函数,我们称之为初等函数,主要由以下一些。
- 幂函数:y=x^n
- 指数函数:y=a^x
- 对数函数:y=\log_a x
- 三角函数:正弦函数y=\sin x,余弦函数y=\cos x,正切函数y=\tan x等。
- 反三角函数:如反正弦函数y=\arcsin x,反余弦函数y=\arccos x等。
这就是微积分中函数的概念。