闭区间是指区间两端闭合的区间,例如[a,b]是一个闭区间,而(a,b)是一个开区间。
函数在闭区间上连续,就是指函数f(x)在开区间(a,b)内连续,在右端点b左连续,在左端点a右连续。
在闭区间上连续的函数有以下三个重要性质。
有界性与最大值最小值定理
有界性与最大值最小值定理:在闭区间上连续的函数在该区间上有界且一定能取得最大值和最小值。
证明:略。
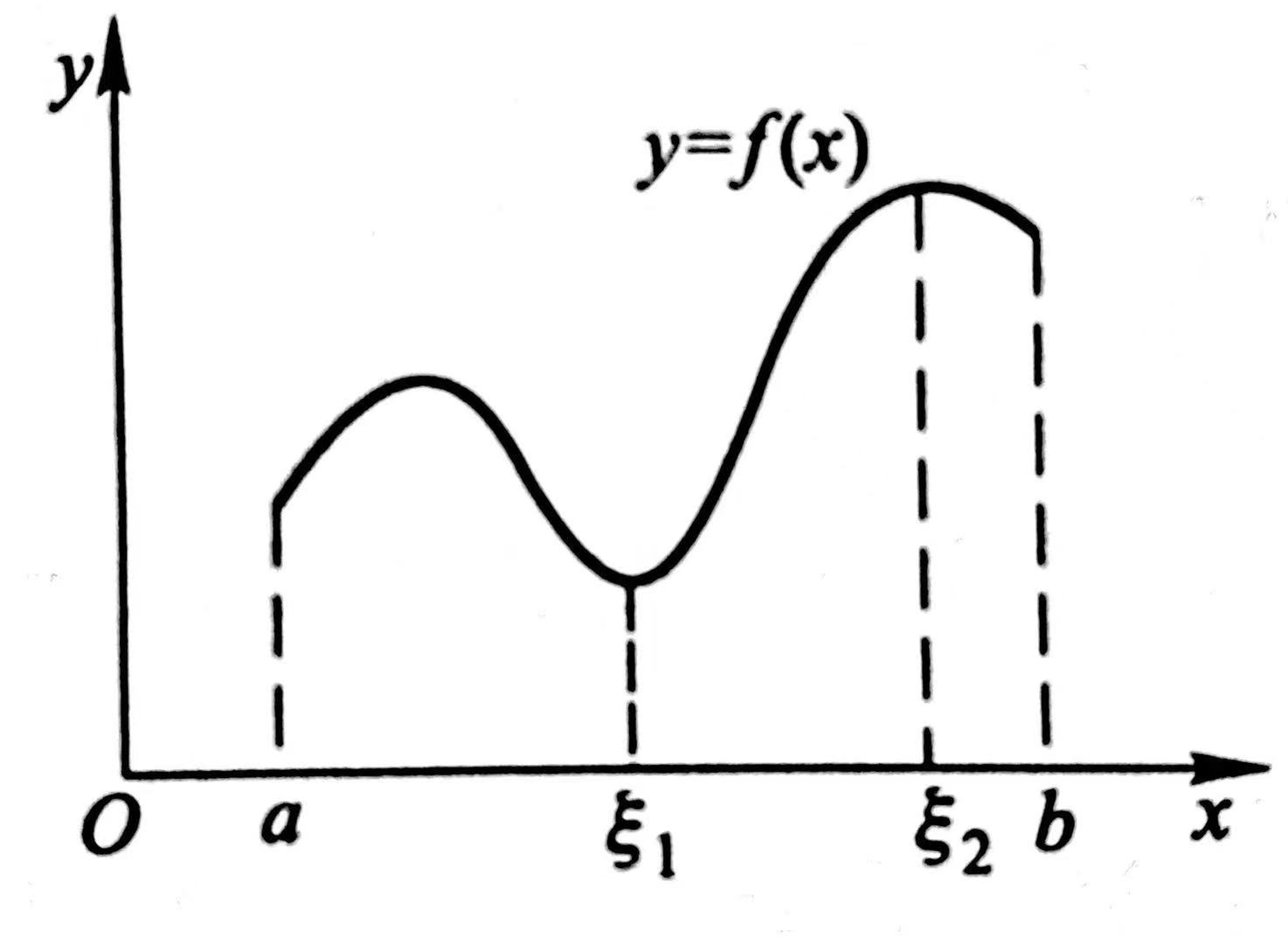
从上图中可以看出,如果函数f(x)在闭区间[a,b]上连续,那么存在常数M>0,使得对于任一x\in[a,b],满足|f(x)|\leq M;
且至少有一点\xi_1,使得f(\xi_1)是f(x)在[a,b]上的最大值;
又至少有一点\xi_2,使得f(\xi_2)是f(x)在[a,b]上的最小值。
零点定理
在讲零点定理之前,先要弄清楚什么是零点?
如果f(x_0)=0,那么x_0就是函数f(x)的零点。
零点定理:设函数f(x)在闭区间[a,b]上连续,且f(a)与f(b)异号,即f(a)\cdot f(b)<0,则在开区间[a,b]内至少有一点\xi,使得f(\xi)=0.
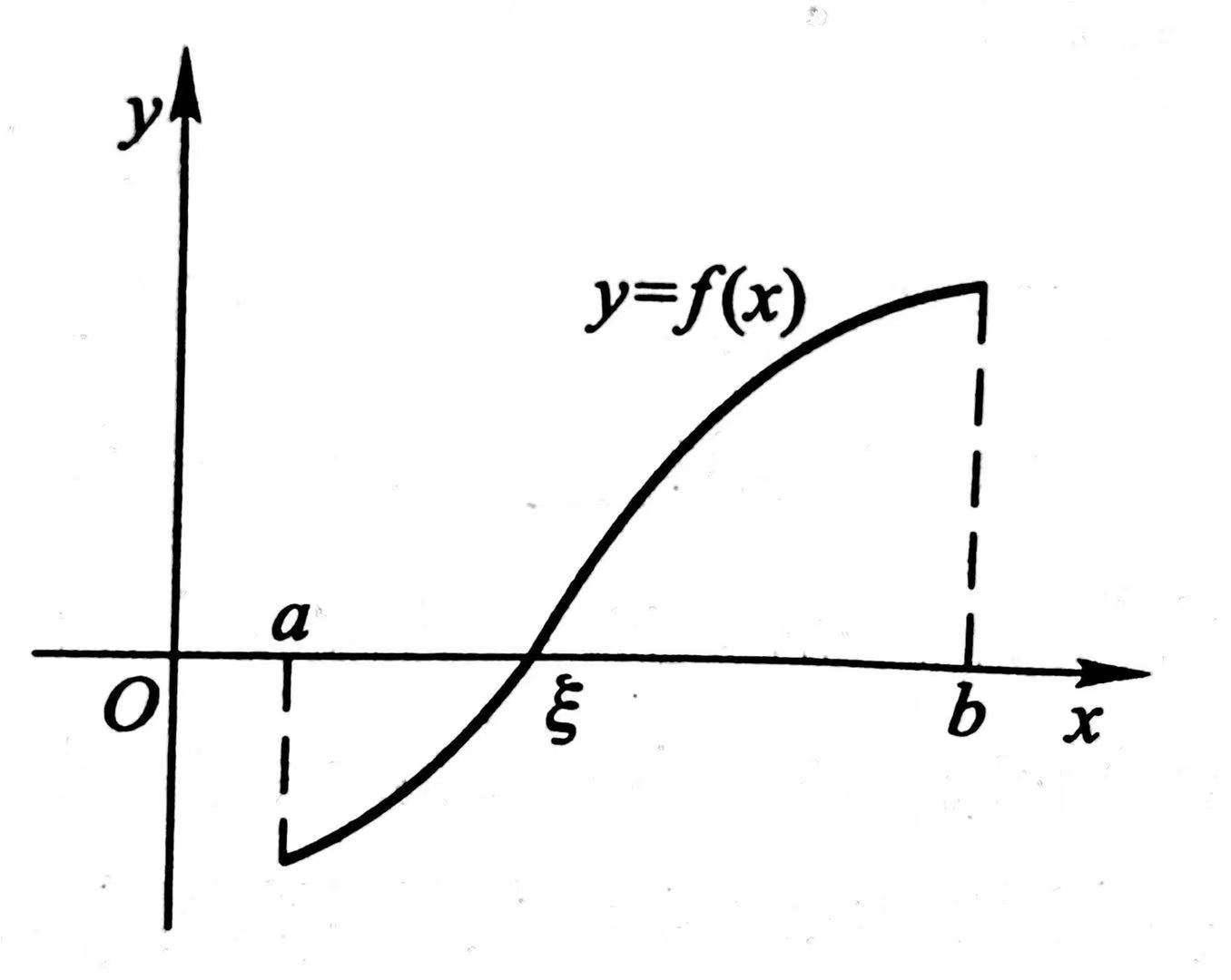
从上图中可以看出,如果连续函数曲线y=f(x)的两个端点位于x轴的两侧,则这段函数曲线与x轴至少有一个交点,即零点。
介值定理
除了零点定理之外,还有一个更一般的定理,介值定理。
介值定理:设函数f(x)在闭区间[a,b]上连续,且在这区间的端点取不同的函数值f(a)=A及f(b)=B,则对于A与B之间的任意一个数C,在开区间(a,b)内至少有一点\xi,使得
f(\xi)=C(a<\xi<b)
介值定理的几何意义就是:连续曲线弧y=f(x)与水平直线y=C至少相较于一点,如下图所示。
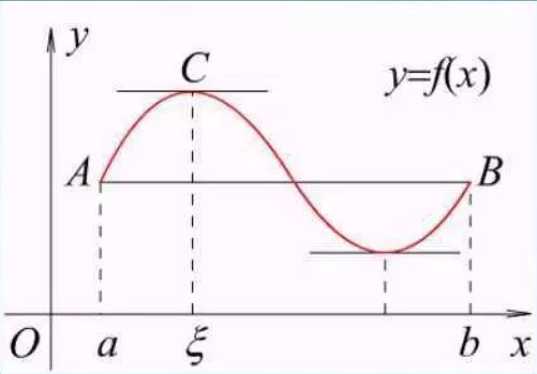
证明:
设\varphi(x)=f(x)-C,则\varphi在闭区间[a,b]上连续,且\varphi(a)=A-C与\varphi(b)=B-C异号。
根据零点定理,开区间(a,b)内至少有一点\xi使得
\varphi(\xi)=0 \quad (a<\xi<b)
又因为\varphi(\xi)=f(\xi)-C,因此由上式可得
f(\xi)=C \quad (a<\xi<b)
一致连续性(选学)
一致连续性的定义:设函数f(x)在区间I上有定义.如果对于任意给定的正数\epsilon,总存在正数\delta,使得对于区间I上的任意两点x_1,x_2,当|x_1-x_2|<\delta时,有
|f(x_1)-f(x_2)|<\epsilon
那么称函数f(x)在区间I上一致连续。
有了一致连续性这个概念之后,还有一个关于一致连续性的定理。
一致连续性定理: 如果函数f(x)在闭区间[a,b]上连续,那么这个函数在该区间上一致连续。
一致连续性表示,不论在区间I的任何部分,只要自变量的两个数值接近到一定程度,就可使对应的函数值达到所指定的接近程度。
以上就是闭区间上连续函数的性质。