前面学习了拉格朗日中值定理,即如果连续曲线在区间[A,B]上可导且连续,那么在该曲线上至少有一点C,使得曲线在点C处的切线平行于弦AB.
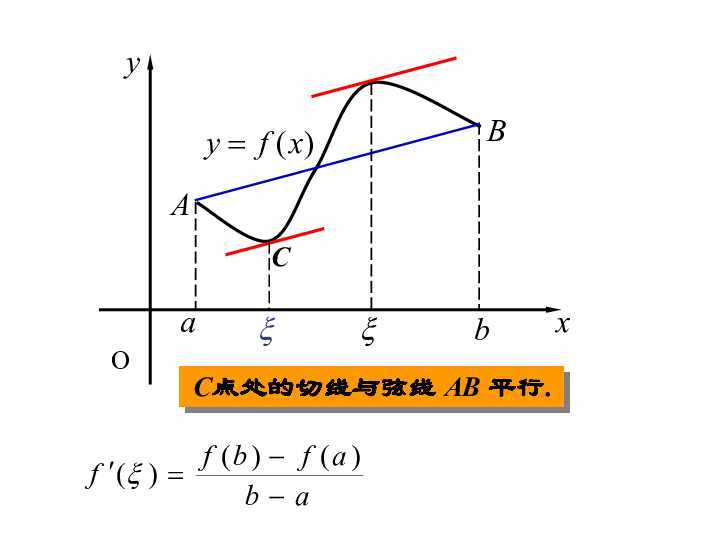
如果将该曲线方程写成参数方程的形式,即
\begin{cases}
x=\varphi(t) \\
y=\psi(t)
\end{cases}
其中,a\leq t\leq b,则曲线上某点(x,y)出的切线的斜率为
\frac{dy}{dx}=\frac{\psi'(t)}{\varphi'(t)}
而弦AB的斜率为
\frac{\psi(b)-\psi(a)}{\varphi(b)-\varphi(a)}
假设点C对应参数t=\xi,那么曲线上点C处的切线平行于弦AB可以表示为
\frac{\psi(b)-\psi(a)}{\varphi(b)-\varphi(a)}=\frac{\psi'(\xi)}{\varphi'(\xi)}
这就是函数在参数方程形势下的拉格朗日中值定理的表达形式,其实就是所谓的柯西中值定理。
柯西中值定理 如果函数f(x)及F(x)满足以下三个条件:
(1)在闭区间[a,b]上连续;
(2)在开区间(a,b)内可导;
(3)对任一x\in(a,b),F'(x)\neq 0,
那么在(a,b)内至少有一点\xi,使等式
\frac{f(b)-f(a)}{F(b)-F(a)}=\frac{f'(\xi)}{F'(\xi)}
成立.
要想证明这个定理也很简单,首先需要引入辅助函数
\varphi(x)=f(x)-\frac{f(b)-f(a)}{F(b)-F(a)}F'(\xi)
当然,这里的F(b)-F(a)\neq 0,因为
F(b)-F(a)=F'(\eta)(b-a)
其中a<\eta<b,根据假定F'(\eta)\neq 0,而b-a\neq 0,所以F(b)-F(a)\neq 0.
回到辅助函数,\varphi(x)在闭区间[a.b]上连续,在开区间(a,b)内可导,且
\varphi(a)=\varphi(b)=\frac{F(b)f(a)-F(a)f(b)}{F(b)-F(a)}
根据罗尔定理,在(a,b)内至少有一点\xi,使得
\varphi'(\xi)=f'(\xi)-\frac{f(b)-f(a)}{F(b)-F(a)}F'(\xi)=0
所以
\frac{f(b)-f(a)}{F(b)-F(a)}=\frac{f'(\xi)}{F'(\xi)}
证毕.
在以上公式中,如果取F(x)=x,则F(b)-F(a)=b-a,F'(x)=1,则以上公式变为
f(b)-f(a)=f'(\xi)(b-a)\quad (a<\xi<b)
这不就是拉格朗日中值定理的公式吗?
所以,拉格朗日中值定理是柯西中值定理的特殊情形。