导数,是微积分中的一个重要概念,导数,也叫微商,当然不是微信中的微商,而是两个微小的差值作商,用公式表示如下:
\lim_{x\rightarrow x_0}\frac{f(x)-f(x_0)}{x-x_0}
当x\rightarrow x_0时,分子是一个微小的差值,分母也是一个微小的差值,两者作差,得到的就叫作微商,我们称之为导数。
切线问题
然而,什么是导数呢?从几何的角度看,导数就是切线的斜率。
例如,如下图所示的曲线,任取一点M,再任取另外一点N,用一条直线连接这两点,这条直线叫作割线。
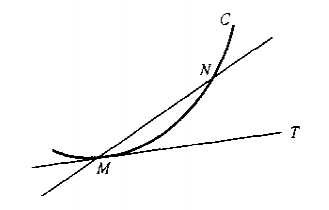
假设点M的横坐标为x_0,点N的横坐标为x,如下图所示。
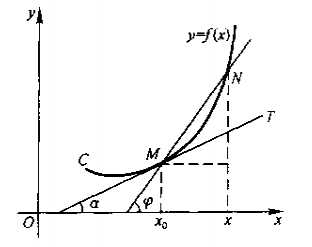
则割线AB的斜率为:
\tan \varphi=\frac{y-y_0}{x-x_0}=\frac{f(x)-f(x_0)}{x-x_0}
保持点x_0不动,让点x不断趋近于点x_0,这条割线就会变化,当点x无限趋近于点x_0时,这条割线就会与曲线相切,我们称之为切线,如下图所示。
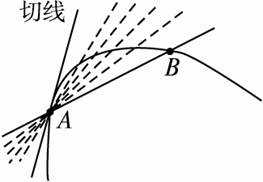
切线的斜率用以下极限表示:
k=\lim_{x\rightarrow x_0}\frac{f(x)-f(x_0)}{x-x_0}
上式中,极限k就是割线斜率的极限,也就是切线的斜率。
导数的定义
以下给出导数的定义:
设函数y=f(x)在点x_0的某个领域内有定义,当自变量x在x_0处取得增量\Delta x,相应地,因变量取得增量\Delta y=f(x_0+\Delta x)-f(x_0),如果\Delta y与\Delta x之比当\Delta x\rightarrow 0时的极限存在,那么称函数y=f(x)在点x_0处可导,并称这个极限为函数y=f(x)在点x_0处的导数,记为f’(x_0),即
f'(x_0)=\lim_{\Delta x\rightarrow 0}\frac{\Delta y}{\Delta x}=\lim_{\Delta x\rightarrow 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}
导数也可以记作
y’|_{x=x_0},\frac{dy}{dx}|_{x=x_0}
或
\frac{df(x)}{dx}\big|_{x=x_0}
在实际生活中,经常遇到的变化快慢的问题本质就是导数的问题,例如速度的变化快慢,即加速度,而加速度其实就是速度的导数,反映了速度变化的快慢。
求导举例
例1:求函数f(x)=C的导数。
解:
f'(x)= \lim_{h\rightarrow 0}{\frac{f(x+h)-f(x)}{h}=\lim_{h\rightarrow 0}{\frac{C-C}{h}=0}}
也就是说,常数的导数等于零。
例2:求函数f(x)=x^n的导数。
解:
当n=1时,
f'(x)=\lim_{h\rightarrow 0}{\frac{f(x+h)-f(x)}{h}}=\lim_{h\rightarrow 0}{\frac{(x+h)-x}{h}}=1
当n>1时,
\begin{aligned}
f'(x)&=\lim_{h\rightarrow 0}{\frac{f(x+h)-f(x)}{h}}=\lim_{h\rightarrow 0}{\frac{(x+h)^n-x^n}{h}} \\
& =\lim_{h\rightarrow 0}{[nx^{n-1}+\frac{n(n-1)}{2}x^{n-2}h+\cdots+h^{n-1}]=nx^{n-1}}
\end{aligned}
总之,有以下结论。
(x^n)’=\begin{cases}
1, \quad n=1 \\
nx^{n-1}, \quad n>1
\end{cases}
以上就是微积分中的导数。