对于极限是否存在来说,有两个重要的准则:夹逼准则和单调有界准则。
准则1:夹逼准则
我们先来看第一个准则:夹逼准则,由于极限分为数列极限和函数极限,所以夹逼准则也分为这两个方面来说。
准则1:如果数列\lbrace x_n \rbrace,\lbrace y_n \rbrace及\lbrace z_n \rbrace满足下列条件:
(1)从某项起,即\exist n_0\in \N_+,当n>n_0时,有y_n\leq x_n\leq z_n;
(2)\lim_{n\rightarrow\infty}y_n=a,\lim_{n\rightarrow\infty}z_n=a,
那么数列\lbrace x_n \rbrace的极限存在,且\lim_{n\rightarrow\infty}x_n=a.
证明:
因为y_n \rightarrow a,z_n \rightarrow a,所以根据数列极限的定义,\forall \epsilon>0,\exist N_1,当n>N_1时,有|y_n-a|<\epsilon;
对于z_n,\exist N_2,当n>N_2时,有|z_n-a|<\epsilon.
取N=\max \lbrace n_0,N_1,N_2 \rbrace,则当n>N时,有
|y_n-a|<\epsilon, \quad |z_n-a|<\epsilon
同时成立,即
a-\epsilon<y_n<a+\epsilon, \quad a-\epsilon<z_n<a+\epsilon
同时成立。
又因为当n>N时,x_n介于y_n和z_n之间,从而有
a-\epsilon<y_n\leq x_n\leq z_n<a+\epsilon
有
|x_n-a|<\epsilon
成立。这就证明了\lim_{n\rightarrow\infty}x_n=a。
当然,上述准则对于函数极限也成立。
如果:
(1)当x\in \mathring U(x_0,r)时,g(x)\leq f(x)\leq h(x);
(2)\lim_{x\rightarrow x_0}g(x)=A,\lim_{x\rightarrow x_0}h(x)=A,
那么\lim_{x\rightarrow x_0}f(x)=A.
以上定理称为夹逼准则,或者夹逼定理。
两个重要极限
利用夹逼定理又可以推出一个重要的极限。
\lim_{x\rightarrow 0}\frac{\sin x}{x}=1
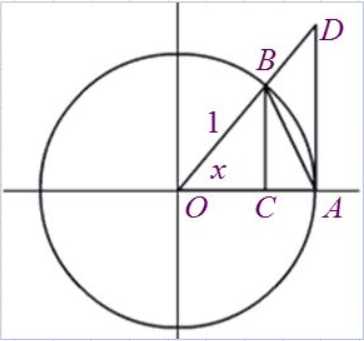
设圆心角\angle AOB=x(0<x<\frac{\pi}{2}),则
\sin x=CB, \quad x=\widehat{AB}, \quad \tan x=AD
从图中很容易看出,三角形AOB的面积<扇形AOB的面积<三角形AOD的面积
所以
\frac{1}{2}\sin x<\frac{1}{2}x<\frac{1}{2}\tan x
即
\sin x<x<\tan x
在以上不等式中除以\sin xx,得
1<\frac{x}{\sin x}<\frac{1}{\cos x}
或
\cos x<\frac{\sin x}{x}<1
对以上不等式两边取极限,即得
\lim_{x\rightarrow 0}\frac{\sin x}{x}=1
证毕。
准则2:单调有界准则
第二个准则比较简单,一句话:单调有界数列必有极限。
单调表示数列单调递增或者单调递减。
利用和这个准则可以推出另一个重要极限:
\lim_{x\rightarrow\infty}(1+\frac{1}{x})^x=e
说明:$e$是一个无理数,值为:$e=2.718 281 828 \cdots$
例如,求下列极限
\lim_{x\rightarrow \infty}(1-\frac{1}{x})^x
解:
令t=-x,则当x\rightarrow \infty时,t\rightarrow -\infty。于是
\lim_{x\rightarrow \infty}(1-\frac{1}{x})^x=\lim_{t\rightarrow -\infty}(1+\frac{1}{t})^{-t}=\lim_{t\rightarrow -\infty}\frac{1}{(1+\frac{1}{t})^t}=\frac{1}{e}
柯西极限存在准则
前面的单调有界准则给出了数列极限存在的条件,也就是数列收敛的条件,但是收敛数列未必是单调的,所以有柯西极限存在准则。
柯西极限存在准则:数列\lbrace x_n \rbrace收敛的充分必要条件:对于任意给定的正数\epsilon,存在正整数N,使得当m>N,n>N时,有
|x_n-x_m|<\epsilon.
证明:
必要性。
设\lim_{n\rightarrow \infty}x_n=a.\forall \epsilon>0,由数列极限的定义,\exist N,当n>N时,有
|x_n-a|<\frac{\epsilon}{2}
同理,当m>N时,有
|x_m-a|<\frac{\epsilon}{2}
因此,当m>N,n>N时,有
\begin{aligned}
|x_n-x_m|&=|(x_n-a)-(x_m-a)| \\
& \leq |x_n-a|+|x_m-a|<\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon
\end{aligned}
充分性。
略。
以上就是极限存在的两个准则,以及由其推出的两个重要极限。