所谓微积分,其实分为两部分:微分和积分。
例如,要求一个不规则形状的面积,如下图所示,一条函数曲线下方的面积。
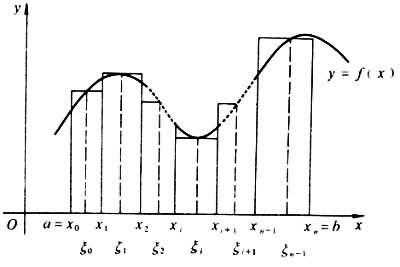
这种不规则图形的面积没有公式可用,我们可以用微积分的思想来考虑。
分两步:微分和积分。
第一步,微分,就是大事化小,将这个不规则图形划分为很多个矩形,每个矩形的高度不同。
第二步,积分,就是积少成多,将划分形成的矩形面积加起来,就等于这个不规则图形的面积。
这个就是微积分的基本思想。
以上这个曲线是一个函数曲线,本文先介绍函数的微分。
考虑一个具体问题:一块正方形金属薄片,其边长由x_0变化到x_0+\Delta x,问此薄片的面积变化了多少?
设薄片的边长为x,面积为A,则有函数关系:A=x^2。
当边长由x_0变化到x_0+\Delta x,面积的增量为\Delta A,有
\Delta A=(x+x_0)^2-x_0^2=2x_0\Delta x+(\Delta x)^2
这只是一个表达式,不太直观,下面通过图形来说明。
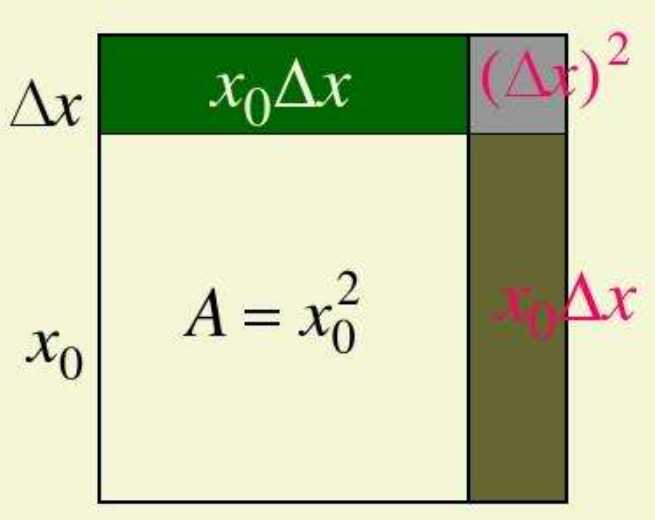
上面这个图清晰地表示了面积增量这个表达式,在上面的公式中,\Delta A分成两个部分,第一部分2x_0\Delta x是\Delta x的线性函数,其实就是图中横竖两个矩形的面积之和,第二部分(\Delta x)^2是图中右上角的小正方形的面积。
当\Delta x\rightarrow 0时,第二部分(\Delta x)^2是比\Delta x高阶的无穷小,即(\Delta x)^2=o(\Delta x)。
由此可见,当边长的改变很微小时,即|\Delta x|很小时,面积的改变量可以近似地用第一部分来代替。
以上这个例子,用数学语言来描述就是:
\Delta A=2x_0\Delta x+o(\Delta x)
一般地,如果函数y=f(x)满足一定条件,那么
\Delta y=A\Delta x+o(\Delta x)
当A\neq 0,且|\Delta x|很小时,我们可以用\Delta x的线性函数A\Delta x来近似代替\Delta y.
下面给出函数的微分的严格定义。
设函数y=f(x)在某区间内有定义,x_0及x_0+\Delta x在这区间内,如果函数的增量
\Delta y=f(x_0+\Delta x)-f(x_0)
可表示为
\Delta y=A\Delta x+o(\Delta x),
其中A是不依赖于\Delta x的常数,那么称函数y=f(x)在点x_0是可微的,而A\Delta x叫做函数y=f(x)在点x_0相应于自变量增量\Delta x的微分,记作d y,即
dy=A\Delta x