数列的极限

极限（limit）是微积分中的一个基本概念，就是无限接近的意思。
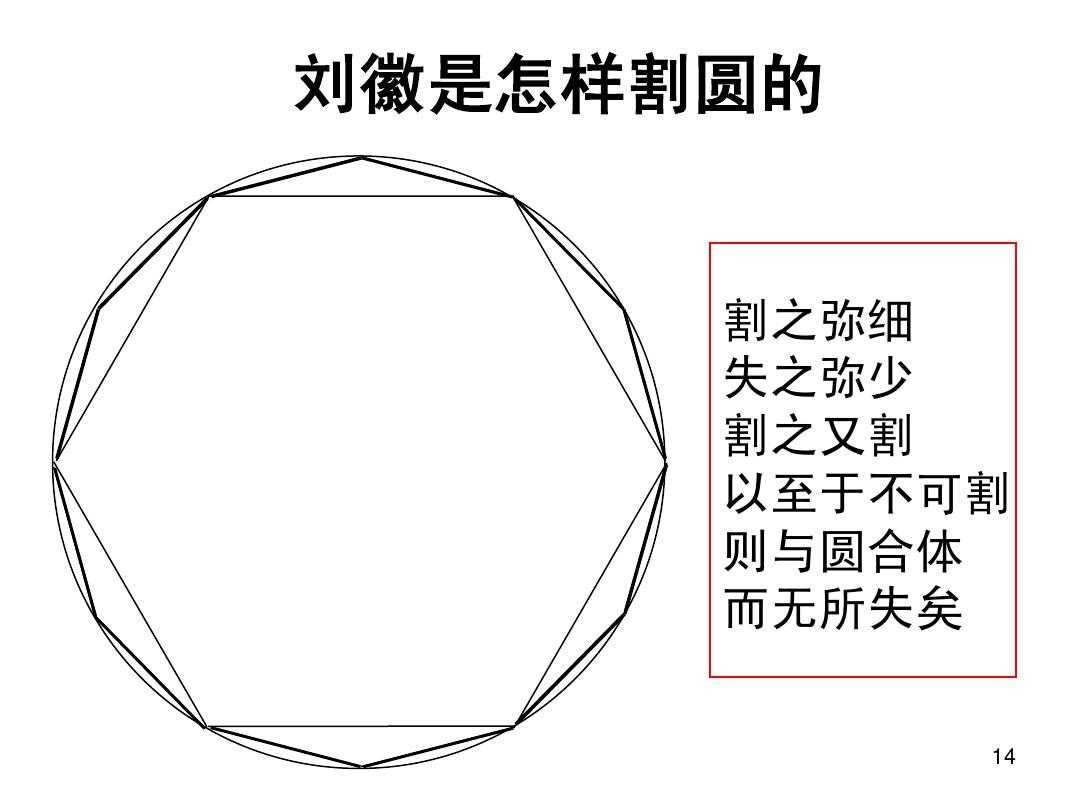
刘徽的割圆术就是利用极限的思想。

数列

数列就是数字序列的意思，例如：
1,2,3,\cdots,n,\cdots就是一个数列，由自然数构成。
例如，2,4,6,\cdots,2n,\cdots，这个数列由偶数构成。
再比如，1,\frac{1}{2},\frac{1}{3},\cdots,\frac{1}{n},\cdots，这个数列由分式构成，即每个自然数取倒数。
对于数列来说，用数学符号表示为：x_1,x_2,\cdots,x_n,\cdots
简记为：\lbrace x_n\rbrace，n表示数列的序号，或者脚标，取值为：1,2,3,\cdots,n，记为：n=1,2,3,\cdots,n,\cdots

数列的极限

接着，来说说数列的极限，就是当n无限增大时，数列的值x_n究竟会怎样，也就是说数列的极限是什么。
显然，对于自然数数列\lbrace n \rbrace来说，当n无限增大时，数列的值会趋于无穷大，我们说这个数列是发散的，它没有极限，或者说极限是无穷大。
对于这个数列\lbrace \frac{1}{n} \rbrace，当n无限增大时，数列的值会趋于零，我们说这个数列是收敛的，它的极限就是零。
用数学语言表达为：

\lim_{n\rightarrow\infty}x_n=0

也就是说对于收敛数列来说，极限存在。
以下给出数列极限的定义：
给定数列\lbrace x_n \rbrace，存在一个常数a，对于任意给定的正数\epsilon（一个很小的数），总是存在正整数N，当n>N时，有|x_n-a|<\epsilon成立，那么，我们称常数a是数列\lbrace x_n \rbrace的极限，记为：

\lim_{n\rightarrow\infty}x_n=a

或者

x_n\rightarrow a(n\rightarrow\infty)

收敛数列的性质

对于收敛数列来说，有以下三条性质。

1. 唯一性：如果数列\lbrace x_n \rbrace收敛，那么它的极限唯一。
   证明：反证法。
   假设同时有x_n\rightarrow a和x_n\rightarrow b，且a<b.
   取\epsilon=\frac{b-a}{2}.
   因为\lim_{n\rightarrow \infty}x_n=a,故\exist N_1，当n>N_1时，不等式

|x_n-a|<\frac{b-a}{2}\qquad(1)

都成立.同理，由于\lim_{n\rightarrow \infty} x_n=b,故\exist N_2，当n>N_2时，不等式

|x_n-b|<\frac{b-a}{2}\qquad(2)

都成立.
取N=\max{N_1,N_2},则当n>N时，以上两式都成立.
但由(1)式得x_n<\frac{a+b}{2},由(2)式得x_n>\frac{a+b}{2},产生矛盾，所以假设不成立.
证毕.

2. 有界性：如果数列\lbrace x_n \rbrace收敛，那么数列\lbrace x_n \rbrace一定有界。
   证明：因为数列\lbrace x_n\rbrace收敛,设\lim_{n \rightarrow}x_n=a.
   根据数列极限的定义，对于\epsilon=1,\exist N,当n>N时,不等式|x_n-a|<1都成立.
   于是，当n>N时，

|x_n|=|(x_n-a)+a|\leq |x_n-a|+|a|<1+|a|

取M=\max \lbrace |x_1|,|x_2|,\cdots,|x_N|,1+|a| \rbrace,那么数列\lbrace x_n \rbrace中的一切x_n都满足不等式

|x_n|\leq M

所以，数列\lbrace x_n \rbrace是有界的.

3. 保号性：如果\lim_{n\rightarrow\infty}x_n=a，且a>0，那么存在正整数N，当n>N时，都有x_n>0.

证明：由数列极限的定义，对\epsilon=\frac{a}{2}>0,\exist N,当n>N时，有

|x_n-a|<\frac{a}{2}

从而，

x_n>a-\frac{a}{2}=\frac{a}{2}>0

证毕.
当a<0时，上述性质也成立，证明方法同上。
由上述性质还能得到一个推论：
如果数列\lbrace x_n \rbrace从某项起有x_n\geq 0(或x_n \leq 0),且\lim_{n\rightarrow\infty}x_n=a,那么a\geq 0(或a\leq 0).

好，以上就是微积分中的数列的极限这个知识点。