隐函数是什么?
什么是隐函数?隐函数是相对于显函数来说,显函数就是我们前面提到的函数,例如y=x+1,y=\sin x等,即左边是因变量y,右边是y的表达式。
然后,有些函数却不是这种形式,例如x+1-y=0,当给定一个x时,有一个唯一确定的y值与之对应,只是没有表示成y的某种形式,这种函数就叫作隐函数。
当然,对于这个隐函数x+1-y=0,由于它比较简单,我们很容易将其表示成一个显函数,即y=x+1,这个过程叫作隐函数的显化。
对于很多隐函数,是没有办法直接进行显化的,如果要求导的话,就需要直接对隐函数进行求导。
这就涉及到一个问题:如何对隐函数进行求导?
举个例子。
例1:求由方程e^y+xy-e=0所确定的隐函数的导数\frac{dy}{dx}。
解:在方程两边分别对x求导,得
e^y\frac{dy}{dx}+y+x\frac{dy}{dx}=0
在上述方程中解得
\frac{dy}{dx}=-\frac{y}{x+e^y}\quad(x+e^y\neq 0)
于是,就得到导数。
例2:求由方程y^5+2y-x-3x^7=0所确定的隐函数在x=0处的导数\frac{dy}{dx}|_{x=0}.
解:方程两边对x求导,得
5y^4\frac{dy}{dx}+2\frac{dy}{dx}-1-21x^6=0
从以上方程解得
\frac{dy}{dx}=\frac{1+21x^6}{5y^4+2}
当x=0时,由原方程得y=0,所以
\frac{dy}{dx}|_{x=0}=\frac{1}{2}
由参数方程确定的函数的求导
有很多函数是用参数方程表示的。例如,物理中的斜抛问题,斜向上抛出一个物体,如果忽略空气阻力,则物体会形成一个曲线轨迹,如下图所示。
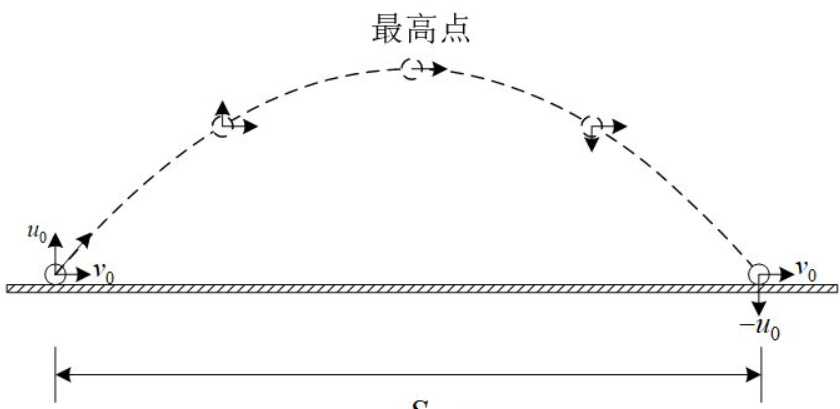
我们可以将物理的运行分解为两个方向上的运行:水平的匀速直线运动和竖直的匀变速运动(竖直速度先增大,达到最高点,再减小到零)。
用运动学公式表示为:
\begin{cases}
x=v_0 t \\
y=u_0 t-\frac{1}{2}gt^2
\end{cases}
这个就是由参数方程所确定的函数。
如果要对这个函数求导,可以消去参数t,得到
y=\frac{u_0}{v_0}x-\frac{g}{2v_0^2}x^2
我们将其化成了显函数,于是可以直接对以上函数求导即可。
然后,对于很多参数方程函数来说,无法直接化成显函数,所以需要找到一种由参数方程确定的函数的求导方法。
假设,给定一个参数方程:
\begin{cases}
x=\varphi(t) \\
y=\psi(t)
\end{cases}
该参数方程确定y与x之间的函数关系。
接下来,求这个由参数方程所确定的函数的导数,假设函数x=\varphi(t),y=\psi(t)都可导,且\varphi(t)\neq 0,于是
\frac{dy}{dx}=\frac{dy}{dt}.\frac{dt}{dx}=\frac{dy}{dt}.\frac{1}{\frac{dx}{dt}}=\frac{\psi'(t)}{\varphi'(t)}
即
\frac{dy}{dx}=\frac{\psi'(t)}{\varphi'(t)}
当然,也可以写成
\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}
举个例子。
例3:已知椭圆的参数方程为:
\begin{cases}
x=a\cos t \\
y=b\sin t
\end{cases}
求椭圆在t=\frac{\pi}{4}相应的点处的切线方程。
解:
当t=\frac{\pi}{4}时,椭圆上的点的坐标是
x_0=a\cos \frac{\pi}{4}=\frac{\sqrt 2a}{2}
y_0=b\sin \frac{\pi}{4}=\frac{\sqrt 2b}{2}
于是,曲线在该点出的切线的斜率为
\frac{dy}{dx}|_{t=\frac{\pi}{4}}=\frac{(b\sin t)’}{(a\cos t)’}|_{t=\frac{\pi}{4}}=\frac{b\cos t}{-a\sin t}|_{t=\frac{\pi}{4}}=\frac{b}{a}
用点斜式表示切线的方程,
y-\frac{\sqrt 2b}{2}=-\frac{b}{a}(x-\frac{\sqrt 2a}{2})
化简后得
bx+ay-\sqrt 2ab=0