罗尔定理,简单来说,就是一个连续可导函数,如果两个端点处的函数值相等,那么中间至少有一点的导数为零。
用图形描述如下图所示。
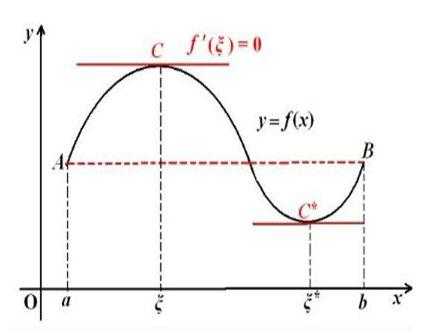
用数学语言描述,就是罗尔定理。
如果函数f(x)满足:
1. 在闭区间[a,b]上连续;
2. 在开区间(a,b)内可导;
3. 在区间端点处的函数值相等,即f(a)=f(b),
那么在(a,b)内至少有一点\xi(a<\xi<b),使得f'(\xi)=0.
把这个定理和上面的图形对照着看,其实很容易理解。
如果想证明这个定理,需要先了解一个引理。
费马引理: 设函数f(x)在点x_0的某领域U(x_0)内有定义,并且在x_0处可导,如果对任意的x\in U(x_0),有f(x)\leq f(x_0)(或f(x)\geq f(x_0)),那么f'(x_0)=0.
证明:
设x\in U(x_0)时,f(x)\leq f(x_0)。
于是,对于x_0+\Delta x\in U(x_0),有
f(x_0+\Delta x)\leq f(x_0)
从而当\Delta x>0时,
\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\leq 0
当\Delta x<0时,
\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\geq 0
根据函数f(x)在x_0可导的条件及极限的保号性,便得到
f'(x_0)=f’_+(x_0)=\lim_{\Delta x\rightarrow0^+}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\leq 0
f'(x_0)=f’_-(x_0)=\lim_{\Delta x\rightarrow0^-}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\geq 0
所以,f'(x_0)=0.
如果f(x)\geq f(x_0),可以类似地证明。
证毕。
这里在介绍一个概念,驻点,通常称倒数等于零的点为函数的驻点(或稳定点)。
有了费马引理,再来说罗尔定理的证明。
证明:根据罗尔定理的条件,f(x)在闭区间[a,b]上连续,根据闭区间上连续函数的最大值最小值定理,f(x)在闭区间[a,b]上必定有最大值M和最小值m。
那么,可能有以下两种情形:
(1)M=m,此时f(x)在闭区间[a,b]上必然取得相同的数值M: f(x)=M,因此,任取\xi\in(a,b),有f'(\xi)=0.
(2)M>m. 因为f(a)=f(b),所以M和m这两个数中至少有一个不等于f(x)在区间[a,b]的端点处的函数值。不妨设M\neq f(a),那么必定在开区间(a,b)内有一点\xi使得f(\xi)=M. 因此,\forall x\in[a,b],有f(x)\leq f(\xi),从而根据费马引理可知f'(\xi)=0.
证毕。