上一节讲了罗尔定理,罗尔定理有个重要条件,就是f(a)=f(b),如果将这个条件去掉,就得到一个新的定理,就是所谓的拉格朗日中值定理。
拉格朗日中值定理: 如果函数f(x)满足以下两个条件:
(1)在闭区间[a,b]上连续;
(2)在开区间(a,b)内可导,
那么在(a,b)内至少存在一点\xi(a<\xi<b),使得等式
f(b)-f(a)=f'(\xi)(b-a)
成立.
这个定理通过图像很容易理解,如下图所示。
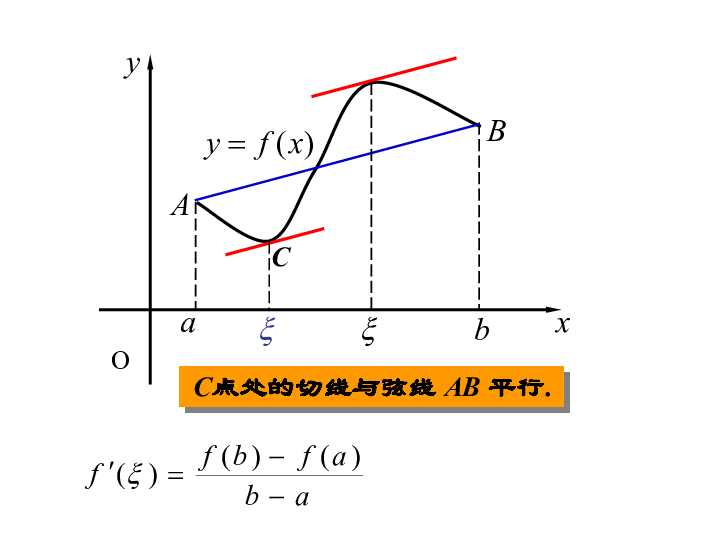
从图中可以看到,\frac{f(b)-f(a)}{b-a}为弦AB的斜率,而f'(\xi)为曲线在点C处的切线的斜率。
这两者相等,也就是说,我们能够在函数曲线上至少找到一点C,使得曲线在C点处的切线平行于弦AB.
当f(a)=f(b)时,其实就是罗尔定理的情形,也就是说罗尔定理是拉格朗日中值定理的特殊情形。
要想证明拉格朗日中值定理,可以借助于前面所讲的罗尔定理。
证明:引入辅助函数
\varphi(x)=f(x)-f(a)-\frac{f(b)-f(a)}{b-a}(x-a)
该函数\varphi(x)符合罗尔定理的条件:
\varphi(a)=\varphi(b)=0, \varphi(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且满足
\varphi'(x)=f'(x)-\frac{f(b)-f(a)}{b-a}
根据罗尔定理,可知在(a,b)内至少存在一点\xi,使\varphi'(\xi)=0,即
f'(\xi)-\frac{f(b)-f(a)}{b-a}=0
所以得到
\frac{f(b)-f(a)}{b-a}=f'(\xi)
即
f(b)-f(a)=f'(\xi)(b-a)
证毕。
当然,对于b<a上述定理也成立。